Game Theory
VI. Sequential Rationality and Sequential
Games with Imperfect Information
Activity 1 : The Market for Lemons [Ali, 129]
Divide class into car dealers and car purchasers evenly
Have dealers decide on absolute minimum price they will accept for a
Good car Ph (price for a high quality car)
Lemon Pl (price for a car which is a lemon, or low quality)
(say we’re selling used 99’ VW Jettas)
Have purchasers decide on absolute max price they will pay for a
High quality H> Ph
Low quality L> Pl
Now, Distribute to dealers G (good) and L (low) quality cars with 50/50 chance for each randomly and make sure every one knows Ph, Pl, H, L. Dealer receives cars and go away and announces price (p) to a specific purchaser. Purchaser then decides whether to purchase or not (they do not know whether or not the dealer has been given a G or L car).
End of Activity
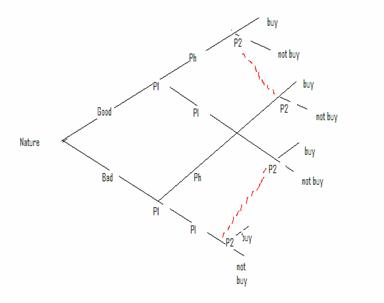
(The red dashed lines indicate where P2 (purchaser) cannot tell the difference in what they are purchasing)
If Pl<p<Ph, the car is a lemon, buy it if you want.
Purchaser not buying gives utility 0.
Buying Utility H-p for good car.
L-p for lemon car.
Equal chance so 1/2 (H-p) + ˝(L-p) >= 0 so if dealer sets price any higher that ˝(H+L) purchaser will not buy.
Case 1:
˝(H+L)>=Ph both G and L offered at this price
Case 2:
˝(H+L)<Ph only lemons offered at this price
Buyer knows this so will only pay L for the car.
Model and discuss.
Activity 2 : Blind Poker (2 Players, 4 Cards (A,K,Q,J))
Each player is given a card and without looking at it puts it up on there forehead for the other player to see. They take turns being the first to act, the one that is not first to act is “blind” with a min bet of 1 the first to act can either bet 1 raise 1 or fold. The “blind” if raised can only call or fold. The player with the highest card wins the pot. Model this game. After giving some thought to this, partner off, and give them each 10 points. Then give them the option of buying the blind or non-blind spot off each other (if someone buys a position they keep it for the remainder of the game (until someone bust)).
End of Activity
Now going back to the market for lemons, how is it that honest dealers are more likely to sell cars? Let’s look at this from a Game Theoretic point of view. Say by chance that they are given a G then they are 90% likely to set the price Ph and 10% likely to set Pl, and given a L only 10% to set Ph and 90% to set Pl, so a rather honest seller. So we have
Exp(not buy)=0
Exp(buy)=.5*.9(H-Ph)+.5*.1(H-Pl) + .5*.1(L-Ph)+.5*.9(L-Pl)=.5(H-Ph) + .5(L-Pl)>0
Hence we always buy from this honest dealer.
Signaling Games
You as and Entrepreneur (E,P1) have an idea however, have insufficient funds and are in need of a venture capitalist (V,P2) to develop your idea into a profitable venture. Naturally, you want them to think your idea is valuable but why? Well…
The project is going to require some investment (I), and with some probability (p) will yield a High amount (H) and probability (1-p) a Low amount (L).
To get the Venture Capitalist to finance the idea you must offer them a stake (e), now the must decide to invest in your idea or to invest in a safe investment and receive an interest rate (i).
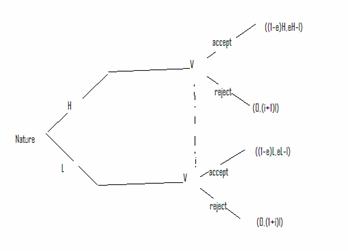
Exp(Reject)=I(1+i)
Exp(Accept)=p(eH-I) + (1-p)(eL-I)
So break even at e*= (2+i)I/(pH+(1-p)L), so e must be >= to this to get V to go, if this amount is >= 1 no go, since there is no incentive for E. Also E wants V to think the project is work H so they have to give them a smaller proportion, they can do this by over estimating H or p.
References and Further
1.C. D. Aliprantis,
and S. K. Chakrabarti, Games and Decision Making,
University Press,
2. P. Straffin, Game Theory and Strategy, The Mathematical Association of
1993.