Game Theory

III. Strategic moves in Matrix Games

Recall again the Prisoner’s Dilemma from Lecture 1, but let us name P1 Jason and P2 Peter. Jason and Peter have been arrested for a crime and both are now sitting in holding cells awaiting questioning. Recall that the NE for this game is (Confess, Confess), but what would be best for both Jason and Peter is (Silent, Silent).

A Pareto optimal strategy is a strategy pair which is better for both players.

But, however to get there Jason will have to make a promise that if Peter plays S, so will he.

Def: Promise

1) Jason will take an action based on a previous action by Peter

2) Jason’s action will benefit Peter

3) Jason’s action will be harmful to Jason.

Now, if Peter believes Jason’s promise, his choice is between (Silent, Silent) and (Confess, Confess). He will clearly choose (S, S), and both are happy.

Threats in Matrix Games

Consider the game

Strategy	A	B
A	(4,3)	(3,4)
B	(2,1)	(1,2)

With, again, P1 being Jason and P2 being Peter. The solution to this game is

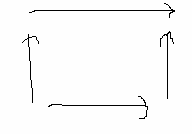
So the NE in pure strategies is (A,B), it is also Pareto optimal. Suppose Peter must go first and Jason makes the threat “If you choose B so will I.”

Def: Threat

1) Jason says he will do something based on an action by Peter

2) Jason’s action will be harmful to Peter

3) Jason’s action will be harmful to Jason

If Peter believes Jason’s threat, he can choose between BB and AA. Peter would prefer AA, in which case Jason would receive his highest payoff.

Notice that in the Prisoners Dilemma game threats will not work!

Example: A game with NE which is vulnerable to a threat and promise.

Consider

Strategy	A	B
A	(3,3)	(1,5)
B	(4,0)	(0,2)

With solution

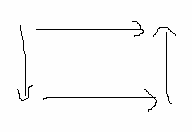
The NE is then (A,B).

Suppose Jason threatens “If you choose B so will I”. This is ineffective, since if Peter does choose A then Jason is better off playing B, so Peter with this threat can choose between (B,A) and (B,B), but prefers (B,B).

Suppose Jason promises “If you choose A, so will I”. This too is ineffective, since Peter can choose between (A,A) and (B,A) (if B then Jason prefers B). So Peter will prefer to ignore this and take (B,A).

However, Jason could simultaneously give the threat and promise, in which case, Peter must choose between (A,A) and (B,B), from which he would prefer (A,A). So Jason has managed to get a significantly higher payoff.

The problem is that both threats and promises require for that player’s action to be harmful to themselves, and for these to work the other player must believe them.

Increasing Credibility:

1) Pledge your honor

2) Have a witness, and if you fail to keep the Threat/Promise, you will forever lose credibility

3) Sign a contract to pay some fixed amount to a 3^rd party if you fail to keep the agreement

(*) idea, all three of these reduce the player’s utility for going against the “deal”

In the last game, Jason could make his threat more credible by lowering (A,B) from 1 to

-1. Jason could also make his promise more credible by lowering (B,A) from 4 to 2.

Weird: It can be an advantage in a game to lower some of your payoffs.

Games of Repeated Play

When Players can communicate, they can use repeated play to establish credibility of there threats and promises.

Without communication players can go TIT for TAT (for example as can be done in the iterated Prisoner’s Dilemma), even if players cannot communicate, they can make implicit strategy moves such as “If you cooperate, so will I”

(*) Strategic moves can be conveyed quite effectively in iterated play even if the players don’t know each other’s payoffs. Such as in the adjoined game from [Str, 89].

Activity : This game will require a partner (not necessarily one who has been studying with you). If you are working through these lectures in a classroom setting, the students should pair off.

For this game you will need the students to pair off. One will be a Wholesaler and the other a Retailer. Separate the two types of people into two groups and make sure that the groups of Wholesalers and Retailers don’t collaborate. This game is the “Wholesaler vs. Retailer” in a bilateral monopoly.

To the Wholesaler(s) give the following handout.

The Wholesaler's Game						Profit to Wholesaler in round #
		Wholesaler's Price
Retailer's Order		$9	$10	$11	$12
	0	0	0	0	0	1
	8	22	27	34	42	2
	16	32	42	56	70	3
	20	30	42	61	78	4
	28	26	43	69	93	5
						6
						7
						8
						9
						10
						11
						12
						13
						14
						15
						Total

To the Retailers give this worksheet.

The Retailer's Game						Profit to Retailer in round #
		Wholesaler's Price
Retailer's Order		$9	$10	$11	$12
	0	0	0	0	0	1
	8	28	23	16	8	2
	16	48	38	24	10	3
	20	54	42	23	6	4
	28	62	45	19	-5	5
						6
						7
						8
						9
						10
						11
						12
						13
						14
						15
						Total

The goal of the game is for each player to maximize there profits. Round 1 starts with the wholesaler writing down a price for delivery to their retailer, then the retailer places an order and each record there profits (on the worksheet below). Make sure that the price and order amount is the only communication between partners.

Pair #
		Wholesaler's price			Retailer's order
Round	1		Round	1
	2			2
	3			3
	4			4
	5			5
	6			6
	7			7
	8			8
	9			9
	10			10
	11			11
	12			12
	13			13
	14			14
	15			15

End of Activity

Some of the points on these payoff points can be classified.

1) Resistance Points, where the retailers were resisting the wholesaler’s prices by placing small orders, to try to get wholesalers to lower prices next round. In the Wholesaler’s payoff matrix these are

2) Bowley Points, If both knew each other’s payoffs and the wholesaler went first, the outcome would be these.

3) Equal Profits, If the players could see each other’s profits and were trying to be “fair”, they would be attracted to these points.

After completing the game have a discussion so that students can express there thought process about how they were making there decisions. I found that the personalities that they had expressed, prior to this game, were accurately reflected in how aggressive or passive the students were.

References and Further Reading:

1.C. D. Aliprantis, and S. K. Chakrabarti, Games and Decision Making, Oxford

University Press, New York, 2000.

2. P. Straffin, Game Theory and Strategy, The Mathematical Association of America, DC,

1993.