Knot theory
I. Introduction
Section1. What is a knot?
With a reasonably long, say 30cm in length, piece of string or cord in your hand, straighten it up, take the two ends and glue them together so that it is not immediately noticeable that the string/cord has been joined. Now what you see before you is a single closed loop, approximately 30cm long. In mathematics, this loop is called a trivial knot or unknotted knot, which is a simple closed loop. You should be able to deform it to a circle at ease, fig.3.
Fig.3. In knot theory, these two knots are equivalent.
It is the simplest knot in our world. More generally, before gluing the two ends of the string, you can tie the string in any way you like. As we said before, it always happens in reality that we need to tie different things up, for example, see fig.4.

Fig.4. You can glue the two ends at the bottom of the picture to make it a non-simple closed loop. It is called a Tom fool knot.
To be more precise, this string should, ideally, be thought of as a single curve, then a knot is a closed curve, in space. We can make various types of knots that are independent of how we tie the string. Let us create an extremely complicated knot by using a very long piece of string and knotting it in the most muddled fashion we can imagine, for example fig.5:
Fig.5.
Exercise 1.1 Try to make the knot in fig.5. yourself.
Section2. When are two knots ''equivalent'' ?
Now, choose two knots from the various knots you have created in this random manner and call them A and B. The natural question to ask is, (perhaps you may have predicted it at this point)
Can we deform knot A into knot B ?
An approach we may try is to determine how it is possible to change the knot A to knot B. It is intuitively clear that if we are able to physically continuously deform knot A to knot B, then they are equivalent, for example, see fig1. One condition we impose here is that we cannot cut the knot, we can only manipulate it by hand.
If we can change A into B by slowly changing the form of A, then these two knots are said to be equivalent or equal.
At this point, let us further restrict our notion of knot. Since what we are interested in is the actual form of the knot, we do not need to worry about how long of how thick the knot is. Let us mull a bit over the way we wish to consider a knot. It is perfectly possible that a knot made from a 30cm piece of string is equivalent to a knot made from a 10cm piece of string. Recall, we want to say that two knots A and B are equivalent if we can manipulate, using our hands, the knot A into the knot B. (to visualize this, it is best to suppose the strings have a certain amount of elasticity so that we can stretch and shrink them without any difficulty) So the crux of our problem will lie in the form of knot, not in how thick or long it is. The reader familiar with advanced mathematics (of course, you are not assumed to have this background) will notice that this discussion is just the type of problem encountered in topology. To put it plainly, knot theory, at the very least, may be considered to be a branch of topology.
Example The following knot is equivalent to a trivial knot.
Exercise 1.2 By manipulations using your hands, show that the following knot (due to Ochiai) is equivalent to a trivial knot, a circle.
Fig.6.
The following knot is called trefoil knot:
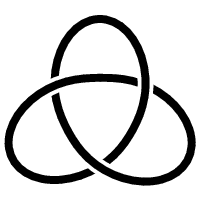
Fig.7. Trefoil Knot
Problem 1.3 We can ask a similar question again: is trefoil knot equivalent to a circle?
The answer is 'no'. However, this will not be an exercise at this point since the proof is far from simple. It could be said that knot theory owes its present development to this very question being asked towards the end of the 19th century. In other words, one aspect of knot theory is to provide the ways and means, to a standard of mathematical rigor, to determine whether two knots are equivalent.
Notice that exercise 1.2 is considerably easy in the sense that it only requires some simple manipulations. But, the fact is, there are infinitely many different knots in the world. It is therefore not a feasible task to manipulate all these random knots by hands in order to determine whether two knots are not equivalent. Hence, mathematics more than just a modicum of intuition and physical manipulation is definitely required to handle these tasks.
We will say a lots more about these things in the later lessons.
Section3. History of knot theory
It is difficult to say who first showed a mathematical interest in what we now call knot theory and when. However, in modern times it is known that the famous mathematician, C.F. Gauss (1777-1855) had some interest in this field, but it was his student, Listing, who undertook research into knot theory and gave significant influence to its later development. Originally, in honour of his accomplishments, the knot now known as the figure 8 knot, fig.8., was called the Listing knot.
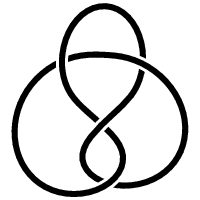
Fig.8. Listing Knot
The American mathematician J.W. Alexander (1888-1971) was the first to show that knot theory is extremely important in the study of topology. This was further underlined by the work of, amongst others, the German mathematician H. Seifert from the late 1920s to the 1930s. In addition, in Germany at this time there was already considerable activity in the study of the relationship between algebraic geometry and knot theory.
After the Second world war, in the 1950s, research into knot theory progressed at a great pace in the United States. Under the influence of this research, there was a great boom of research into knot theory in Japan, which has continued to the present day. In the 1970s, knot theory was shown, among other things, to be connected to algebraic number theory.
At the beginning of the 1980s, due to the discovery by V.F.R. Jones of his epochal knot invariant, knot theory moved from the realm of topology to mathematical physics. As knot theory grows and develops, its boundaries continue to shift. Now, in addition, they overlap certain areas of mathematical biology and chemistry. To expand briefly on this, in biology, certain types of DNA molecules have been experimentally seen to take the form of certain types of knots.
In the lessons that follow, we shall introduce, hopefully in a fairly easy and understandable manner, some mathematics of knot theory and also the relation/application of knot theory to other fields.