Knot theory
VI. More fun stuffs
We are going to see more interesting examples/properties of knot theory , many pictures and descriptions will be provided.
Section1. Perko's Pair
As we have said long before, a knot is perceptively changed if we apply only one elementary knot move. However, if we repeat the process at different places, several times, then the resultant knot seems to be completely different. A famous example, as shown in fig. 47, is called Perko's pair.

fig. 47 Perko's pair
In appearance, Perko's pair of knots looks completely different. In fact, for the better part of 100 years, nobody thought otherwise. However, it is possible to change the left knot to the right knot as shown above, by performing the elementary knot moves a significant number of times. This was only shown in 1970 by the American lawyer K.A. Perko.
For your reference, you can take a look at:
Kenneth A. Perko, Jr. Proceedings of the American Mathematical Society, Vol. 45, No. 2. (Aug., 1974), pp. 262-266.
Section2. Wild knots
We have stressed that we can consider the knot to be an entwined polygon sitting in our space. (That is the reason why we are allowed to draw most of our figures in entwined polygon forms, just like the one in fig. 47) To be mathematically precise, our entwined polygon is a collection of finite number of edges. So, in fact we have been implicitly assuming that the collection of edges in the polygons is finite. At this moment, there is a very natural question to ask: What happens if the number of edges is infinite? The answer is that we may end up with a wild knot.
For an example, see http://upload.wikimedia.org/wikipedia/commons/2/2f/Wild_knot.svg.
Close to the end point, in a sense we may take this to be a 'limit' point, the knot starts to cluster together in a concertina fashion. Some pathological behavior may occur for this kind of knots. Practically, such wild knots are not quite common, so it is sensible to exclude these knots in our previous lessons. Indeed, there are lots of peculiarities when we work within the constraints of such wild knots. For another interesting reference, you can take a look at:
Milnor, J. "Most Knots are Wild." Fund. Math. 54, 335-338, 1964.
Section3. Prime knots
Recall that, in lesson 2, we have learned that knots can be decomposed, in a sense, analogous to the decompositions of natural numbers into prime numbers, into collections of prime knots. So, conceptually speaking, prime knots form the building blocks of all the knots in nature. So it is of absolute importance to find all available prime knots. In general, due to the fact that knots can appear in such a random manners, it can be a nontrivial problem to determine whether a given knot is prime or not. We have already seen some examples of prime knots, for example, the trefoil knot, which has three crossings, and the figure-8 knot, which has four crossings. The trivial knot is not considered as a prime knot. (Just as in natural numbers, 1 is not considered as a prime number). We have known the number of prime knots, up to 10 crossing points
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Number of prime knots with n crossings | 0 | 0 | 1 | 1 | 2 | 3 | 7 | 21 | 49 | 165 |
Unfortunately, we do not have a formula to determine the number of prime knots
for arbitrary values of n.
Section4. Torus knots
We do not have a complete classification of knots yet (recall that a complete knot invariant is not available). The next step is to try to group together knots with a particular property or properties in common, and then try to classify them. One group of knots which have already been completely classified are called torus knots. As the terminology suggests, a knot is a torus knot if it is equivalent to a knot that can be drawn without any points of intersection on the trivial torus. First, we recall the shape of a torus, fig. 48:
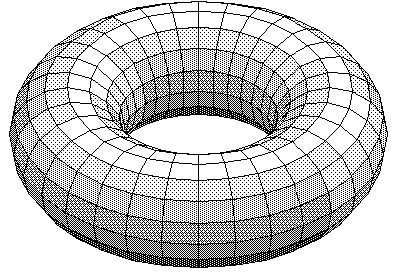
fig. 48 A torus
Each torus knot is specified by a pair of coprime integers p and q. The (p,q)-torus knot winds q times around a circle inside the torus, which goes all the way around the torus, and p times around a line through the hole in the torus, which passes once through the hole, (usually drawn as an axis of symmetry). For examples, see the following figures:
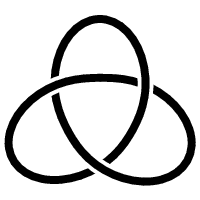
fig. 49 Trefoil knot, a (3,2)-torus knot
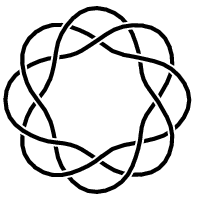
fig.50 a (3,8)-torus knot
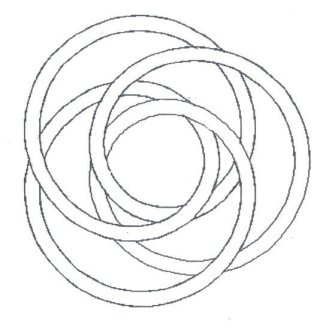
fig.51 a (3,4)-torus knot
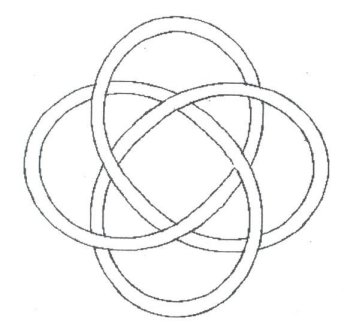
fig. 52 a (4,3)-torus knot
Using the techniques we have discussed in the previous lessons, we are able to completely classify all the torus knots, based on the Jones polynomials. The Jones polynomial of a (p,q)-torus knot is:
![]()
The proof was not too difficult but it involved a lots of tedious calculations so we prefer to skip it here. To conclude, Jones polynomial is a complete invariant for all torus knots. Moreover, it is known that torus knots are prime knots. See [BZ].