What is a Tiling?

Tilings in the World Around Us

Tilings are all around us. Given a bunch of little pieces, it is human nature to wonder how they fit together. In the most general sense of the word, a tiling is just a way of decomposing some space into lots of little pieces (tiles) that fit together without gaps or overlaps. For example, even our bodies can be tought of as tilings in which the "tiles" are cells. Land ownership gives a tiling of the surface of the earth! Tilings are literally everywhere.

Some examples of tilings:

Farm fields "tiling" the surface of the earth Cement road tiles

A stone wall Honeycomb

A brick walkway Onion root tip

Question: Identify ten tilings in the world around you.

The Mathematical Definition of Tilings

As we have seen above, it is possible to "tile" many different types of spaces; however, we will focus on tilings of the plane. By "the plane," we mean the 2-dimensional Euclidean plane -- i.e. a flat, infinitely large surface. From this point on, we will use the word "tiling" to refer to a tiling of the plane.

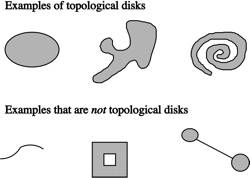
In mathematics, a tiling (of the plane) is a collection of subsets of the plane, i.e. tiles, which cover the plane without gaps or overlaps. There is one more detail to add to this definition – we want a tile to consist of a single connected "piece" without "holes" or "lines" (for example, we don't want to think of two disconnected pieces as being a single tile). Thus, we require that each tile be a topological disk (this is math lingo for "consists of a single connected piece without holes or lines").

We can't draw an entire tiling of the plane (it is of infinite size!), so when we give an illustration of a tiling, it is actually a small piece of the whole tiling.

When Are Two Tilings Equal or Congruent?

Two tiles are said to be congruent if one can be transformed into the other by a rigid motion of the plane, i.e. by a combination of rotations, translations, and reflections (but not stretching/shrinking).

Similarly, two tilings are said to be congruent if one can be transformed into the other by a rigid motion of the plane. Two tilings are said to be equal or the same if one can be changed in scale (magnified or contracted equally throughout the plane) so as to be congruent to the other.

For example, these two tilings are equal (but not congruent since a change of scale is required to make them coincide).