Tilings with Just a Few Shapes

Notice that in our definition of a tiling there is no limit on the number of "shapes" the tiles may be – there could be just a few shapes of tiles, or there might be infinitely many! (Think, for example, of the stone wall and hexagonal brick walkway shown on the first page.)

A monohedral tiling is one in which all the tiles are the same "shape," meaning every tile in the tiling is congruent to a fixed subset of the plane. This set is called the prototile of the tiling, and we say that the prototile admits the tiling. Here are some examples of monohedral tilings.

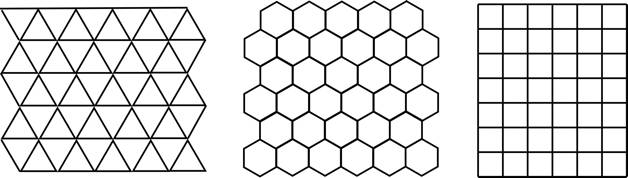
You might think at first that monohedral tilings are necessarily somewhat uninteresting and easy to understand. Not so! Here are two striking monohedral tilings admitted by the same prototile.

In fact, we have no method for determining whether or not a given prototile admits a tiling of the plane! It is even unlikely that such a method could exist!

Of the 24 heptiamonds (a heptiamond refers to seven equilateral triangles stuck together) pictured below, only one is not the prototile of a monohedral tiling. Can you guess which one it is?

A dihedral tiling is a tiling in which every tile is congruent to one or the other of two distinct prototiles. Similarly, trihedral, 4-hedral, ..., n-hedral tilings refer to tilings in which there are 3, 4, ..., n distinct prototiles, respectively.

For example, here is a dihedral tiling whose prototiles are two squares of different sizes:

Question: Show that every pentagon with 2 parallel sides and hexagon with 3 pairs of pairs of equal parallel sides is the prototile of a monohedral tiling.