Monomorphic and

K-Morphic Tilings

So far, we have considered the question of whether or not a given prototile admits a monohedral tiling of the plane. A related question is the following: how many distinct monohedral tilings does a given prototile admit? (Recall that two tilings are said to be equal if it is possible to scale one so that it is congruent to the other. Two tilings are distinct if this is not possible, i.e. if they are not equal.)

For example, here are two distinct monohedral tilings admitted by the same prototile (a square):

However there are some tiles which only admit one tiling. If we modify the square tile in the example above by adding a "zigzag" to each side, there is now only one way to use it to tile the plane.

A tile is called monomorphic if it is the prototile of a unique (i.e. only one) tiling of the plane. For example, this tile

is monomorphic; it is clear that there is only one way to tile the plane with it.

Here are a few more examples of monomorphic prototiles:

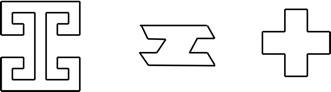
Question: Given an example (not one of the ones above) of a monomorphic prototile.

Question: Show that no triangle can be a monomorphic prototile (i.e. show that you can make more than one distinct monohedral tiling using any triangle.)

Some prototiles admit precisely two distinct monohedral tilings; such tiles are called dimorphic. A prototile is said to be trimorphic if it admits precisely three distinct monohedral tilings, and n-morphic if it admits precisely n distinct monohedral tilings, where n is a positive integer.

An example of two tilings admitted by a dimorphic prototile:

More examples of dimorphic and trimorphic prototiles can be found in "Tilings and Patterns," section 1.5, by Grünbaum and Shephard.

The following two questions are "open" questions, meaning that not even professional mathematicians know the answer yet! (Care to give them a try?)

**Open Question**: for every positive integer n, is it possible to find a tile which is n-morphic?

The next open question uses the idea of countable infinity. An infinite set is said to be countably infinite if the elements of that set are in one-to-one correspondence with the positive integers. In other words, a set is countably infinite if you can make an (infinitely long) list of all the elements of that set.

**Open question**: Does there exist a tile that admits a countable infinity of distinct tilings (but not uncountably many)?

(The square, for example, does not satisfy this question, as it admits uncountably many distinct tilings)