APERIODIC TILINGS

On the previous page we introduced nonperiodic tilings and we gave examples of a monohedral nonperiodic tiling and a dihedral nonperiodic tiling. You may notice that neither of the sets of prototiles is monomorphic (recall that a set of prototiles is monomorphic if it admits only one tiling) – in both cases, we could use the prototiles to construct periodic tilings, as shown below:

nonperiodic periodic

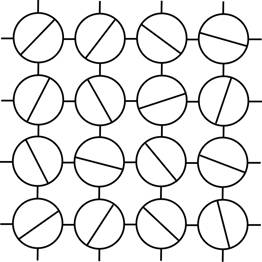
nonperiodic periodic

Thus, a natural question is "Does there exist a finite set of prototiles that admits only nonperiodic tilings?" A set of prototiles with this property (they tile the plane but never periodically) is said to be aperiodic and a tiling admitted by an aperiodic set of prototiles is called an aperiodic tiling. Using this language, the question becomes "Does there exist a finite aperiodic set of prototiles?"

The (somewhat surprising) answer is yes! The first aperiodic set was constructed by Robert Berger in 1966 and used 20,426 prototiles!

The next obvious question is "Can we find a smaller set of aperiodic prototiles?" and, in particular, "What is the smallest number of prototiles necessary to tile the plane aperiodically?" After Berger's discovery, various mathematicians considered this question and discovered sets of aperiodic prototiles with fewer and fewer prototiles.

One well-known set of six aperiodic prototiles was discovered by Robinson in 1971.

But the most famous example of aperiodic tilings are known as Penrose tilings, discovered by Roger Penrose in the 1970s, and have only two prototiles. The section below introduces Penrose tilings. The current record for the lowest number of prototiles in a aperiodic set is two (such as the Penrose tilings); it is not known whether there exists a single prototile that tiles the plane aperiodically.

**Open Question**: Does there exist a single prototile that tiles the plane aperiodically?

Penrose Tilings

Here are the two prototiles in the aperiodic set discovered by Penrose:

The arrows decorating the sides of the tiles indicate the matching rules -- we will require the arrows on adjacent tiles to match in both number and direction. In the context of Penrose tilings, these prototiles are often referred to as the "thin rhomb" and the "thick rhomb."   The interior angles of the thin rhomb are 36° and 144° and the interior angles of the thick rhomb are 72° and 108°. Any tiling constructed using these two prototiles is called a Penrose tiling by thick and thin rhombs.

An example of a Penrose tiling by thick and thin rhombs (the arrows indicating the matching rules are omitted):

Penrose tilings have many amazing properties.

* There are infinitely many Penrose tilings (in other words, there are infinitely many distinct tilings admitted by these two prototiles).

* Not only are Penrose tilings aperiodic, they have no translational symmetry at all – meaning that their group of symmetries does not include a (nonzero) translation in any direction!

* Any finite region of a Penrose tiling occurs infinitely many times in that tiling. In fact, any finite region that occurs in a Penrose tiling appears infinitely many times in every Penrose tiling!

* In 1981 N. G. de Bruijn proved that every Penrose tiling by thick and thin rhombs can be obtained by projecting a five-dimensional cubic structure onto a two-dimensional plane cutting through 5-dimensional space at an irrational angle.