Binomial, Multinomial and Poisson Distribution

Binomial and multinomial distributions are the most frequently used distributions in elementary probability. And they are based on permutations and combinations we studied last time. We begin with a problem:

Problem:A dice is rolled 6 times. What is the probabililty that we will get exactly two 3's?

One way the event can occur is that we have *,3,*,*,3,* as the outcome of experiment in order,where * represents outcome that is not 3. Since rolls are independent of each other, the probability of this pattern occuring is (5/6)(1/6)(5/6)(5/6)(1/6)(5/6)=(5/6)^4*(1/6)^2. Each pattern that contains exactly two '3's corresponds to pick up 2 places out of 6, so the number of different pattens is C_6,2.

We conclude that the probability of getting exactly two '3's is C_6,2*(5/6)^4*(1/6)^2.

Binomial Distribution: The above reasoning can be generalized: We perform a trial independently for n times, and on each trial an event we call 'success' has probability p. Then the probability of k successes out of n trials is

Below are pictures of several examples of binomial distributions and their distribution functions.

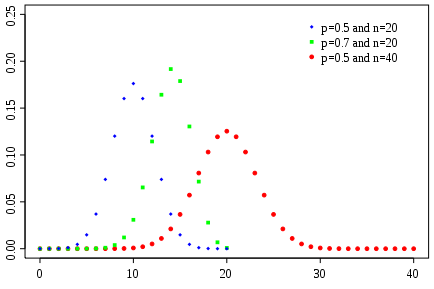
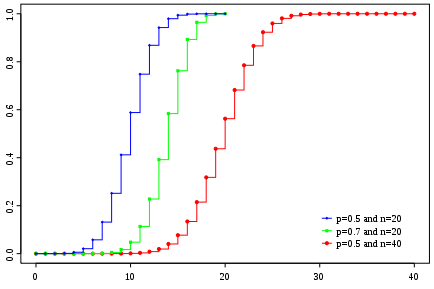
The arguments above generalize easily to independent events with more than two possible outcomes. Again, we begin with a problem:

Problem: Consider a die with 1 painted on three sides, 2 painted on two sides, and 3 painted on one side. If we roll this die ten times what is the probability we get five 1's, three 2's and two 3's?

First, we count the number of patterns to have five 1's, three 2's and two 3's. First, we select 5 places out of 10 and fill them with '1's, then, we select 3 places out of the remaining 5 ,reserved for '2' s, and finally, the places left are for '3' s. So the number of patterns are C_10,5 *C_5,3=10!/(5!*3!*2!). And each pattern appears with probability (3/6)^5*(2/6)^3*(1/6)^2, so the answer is

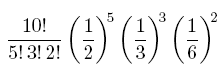
Multinomial Distribution:Generalizing from this example, we see that if we have k possible outcomes for our experiment with probabilities p1,...,pk , then the probability of getting exactly ni outcomes of type i in n = n1 + ...+ nk trials is

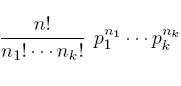
Also binomial and multinomial distributions are not hard to understand, it becomes very troublesome to compute when n is large. But we can use Poisson distribution to approximate binomial distribution when n is large.

Poisson Distribution:X is said to have a Poisson distribution with parameter λ, or Poisson(λ) if

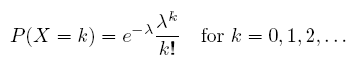
Below are the picture of examles of Poission distribution and their distribution function.

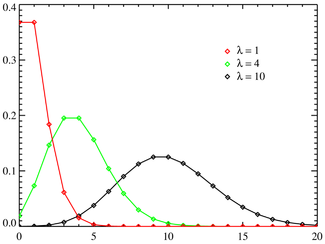
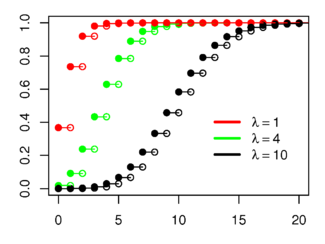
Notice that the distribution function is discontinuous at integers k and flat everywhere else. Because a random variable with Poisson distribution only takes integral values.

Example: Birthday in Ithaca

There are 63 births in Ithaca between March 1st and April 8th, a total of 39 days. The average is 64/39=1.615 per day. The next table gives the number of births per day observed and compares the data to the prediction given by Poisson distribution.

You can see from the table that the prediction is quite good. The next result shows the relation between Poisson distribution and binomial distribution:

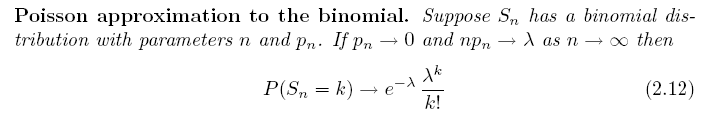
For those who are interested in the proof of the this result, please look it up in R.Durrett's book "Elementary Probability and Applications", Chapter 2.

Maybe you have heard of 'Law of Large Numbers'as an important theorem in probability theory, and there is also a 'Law of Small Numbers' related to Poisson distribution.Roughly speaking, it says that Poisson distribution characterize probability of rare events.In 1898, Ladislaus Bortkiewicz published a book about the Poisson distribution titled " the Law of Small Numbers". In this book he analyzed the number of German soldiers kicked to death by cavalry horses between 1875 and 1894 in each of 14 cavalry corps, arguing that it fit the Poisson distribution. I.J. Good and others have argued that the Poisson distribution should be called the Bortkiewicz distribution, but then it would be very hard to say or write.