return to the Geometric Dissections menu

Three Millennia of Geometric Dissections

Pythagoras’ Theorem

The mathematical result we call today The Pythagorean Theorem was probably known as early as 1800 BC in Mesopotamia, at least in the particular form it takes for a right isosceles triangle. This estimate is based on a clay tablet owned by the Babylonian Collection at Yale University:[1]

The Pythagorean Theorem was certainly known in ancient China and India, possibly long before Pythagoras lived, in Greece. Recently, in an exceptional monograph, Eli Maor writes that there are about four hundred different proofs of the theorem. Some of the oldest, were proofs by dissection.

Pythagoras’s proof is thought to have been made using the following dissection of a square

while a proof given by Bhaskara in India involved this dissection: [2]

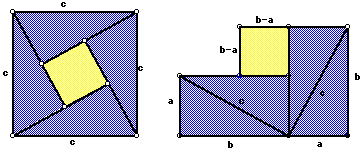
Euclid proved the theorem using the following dissection:[3]

History of mathematics lore has it that Leonardo Da Vinci proved the theorem using a diagram also based on a dissection.[4]

Another famous proof by dissection was given in 19th century by the Frenchman Henry Perigal, who wished the diagram to be drawn on his tombstone: [5]

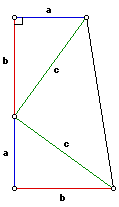
The American president James Abram Garfield (1831-1881), who was assasinated after only 100 days in the higherst American office, apparently proved the theorem by dissecting a right-angle trapezoid: [6]

Plato

In Plato’s dialogue Meno, Socrates uses the dissection of a square by its diagonals to explain his theory of anamnesis, or the recollection of forgotten knowledge. He offers anamnesis in reply Meno’s suggestion that there is no point in seeking knowledge. Meno interrogates the philosophers in a way that later became known as the paradox of knowledge, or the sophistic paradox: “And how are you going to search for [the nature of virtue] when you don’t know at all what it is, Socrates? Which of all things you don’t know will you set up as target for your search? And even if you actually come across it, how will you know that it is that thing which you don’t know?”

Socrates contends that the ‘soul’ is immortal and possesses eternal knowledge but “forgets” it, in the shock of birth. He illustrates his theory by interrogating a slave boy on geometry. He patiently leads the boy to answer correctly to a doubling-of-square question, after skillful questioning makes the boy recognize that his first attempts are wrong. Relevant to us is that Socrates clearly explains (and uses) a dissection of the square by its diagonals.

Let’s read the whole paragraph, despite its length.[7]

Socrates starts by enunciating his theory of recollection. He challenges Meno to witness a conversation between Socrates and a slave boy, and to disprove Socrates’ assertion by finding a contradiction:

Socrates. I told you, Meno, just now that you were a rogue, and now you ask whether I can teach you, when I am saying that there is no teaching, but only recollection; and thus you imagine that you will involve me in a contradiction.
Meno. Indeed, Socrates, I protest that I had no such intention. I only asked the question from habit; but if you can prove to me that what you say is true, I wish that you would.
Socrates.It will be no easy matter, but I will try to please you to the utmost of my power. Suppose that you call one of your numerous attendants, that I may demonstrate on him.
Meno. Certainly. Come hither, boy.
Socrates. He is Greek, and speaks Greek, does he not?
Meno. Yes, indeed; he was born in the house.
Socrates. Attend now to the questions which I ask him, and observe whether he learns of me or only remembers.
Meno. I will.

Now follows the slave boy’s profession of knowledge:

Socrates. Tell me, boy, do you know that a figure like this is a square?
Boy. I do.
Socrates. And you know that a square figure has these four lines equal?
Boy. Certainly.
Socrates. And these lines which I have drawn through the middle of the square are also equal?
Boy. Yes.
Socrates. A square may be of any size?
Boy. Certainly.
Socrates.And if one side of the figure be of two feet, and the other side be of two feet, how much will the whole be? Let me explain: if in one direction the space was of two feet, and in other direction of one foot, the whole would be of two feet taken once?
Boy. Yes.
Socrates. But since this side is also of two feet, there are twice two feet?
Boy. There are.
Socrates. Then the square is of twice two feet?
Boy. Yes.
Socrates. And how many are twice two feet? count and tell me.
Boy. Four, Socrates.
Socrates. And might there not be another square twice as large as this, and having like this the lines equal?
Boy. Yes.
Socrates. And of how many feet will that be?
Boy. Of eight feet.
Socrates. And now try and tell me the length of the line which forms the side of that double square: this is two feet-what will that be?
Boy. Clearly, Socrates, it will be double.

Socrates interrupts the dialogue with the boy for a brief commentary, making sure that Meno follows his argument:

Socrates.Do you observe, Meno, that I am not teaching the boy anything, but only asking him questions; and now he fancies that he knows how long a line is necessary in order to produce a figure of eight square feet; does he not?
Meno. Yes.
Socrates. And does he really know?
Meno. Certainly not.
Socrates. He only guesses that because the square is double, the line is double.
Meno. True.

Next is the refutation of “knowledge”:

Socrates.Observe him while he recalls the steps in regular order. (To the Boy.) Tell me, boy, do you assert that a double space comes from a double line? Remember that I am not speaking of an oblong, but of a figure equal every way, and twice the size of this-that is to say of eight feet; and I want to know whether you still say that a double square comes from double line?
Boy. Yes.
Socrates. But does not this line become doubled if we add another such line here?
Boy. Certainly.
Socrates. And four such lines will make a space containing eight feet?
Boy. Yes.
Socrates. Let us describe such a figure: Would you not say that this is the figure of eight feet?
Boy. Yes.
Socrates. And are there not these four divisions in the figure, each of which is equal to the figure of four feet?
Boy. True.
Socrates. And is not that four times four?
Boy. Certainly.
Socrates. And four times is not double?
Boy. No, indeed.
Socrates. But how much?
Boy. Four times as much.
Socrates. Therefore the double line, boy, has given a space, not twice, but four times as much.
Boy. True.
Socrates. Four times four are sixteen-are they not?
Boy. Yes.
Socrates. What line would give you a space of right feet, as this gives one of sixteen feet;-do you see?
Boy. Yes.
Socrates. And the space of four feet is made from this half line?
Boy. Yes.
Socrates. Good; and is not a space of eight feet twice the size of this, and half the size of the other?
Boy. Certainly.
Socrates. Such a space, then, will be made out of a line greater than this one, and less than that one?
Boy. Yes; I think so.
Socrates. Very good; I like to hear you say what you think. And now tell me, is not this a line of two feet and that of four?
Boy. Yes.
Socrates. Then the line which forms the side of eight feet ought to be more than this line of two feet, and less than the other of four feet?
Boy. It ought.

Now follows a second attempt, which ends in the boy’s recognition of ignorance:

Socrates. Try and see if you can tell me how much it will be.
Boy. Three feet.
Socrates. Then if we add a half to this line of two, that will be the line of three. Here are two and there is one; and on the other side, here are two also and there is one: and that makes the figure of which you speak?
Boy. Yes.
Socrates. But if there are three feet this way and three feet that way, the whole space will be three times three feet?
Boy. That is evident.
Socrates. And how much are three times three feet?
Boy. Nine.
Socrates. And how much is the double of four?
Boy. Eight.
Socrates. Then the figure of eight is not made out of a of three?
Boy. No.
Socrates. But from what line?-tell me exactly; and if you would rather not reckon, try and show me the line.
Boy. Indeed, Socrates, I do not know.

Socrates interrupts again to comment on the dialogue:

Socrates. Do you see, Meno, what advances he has made in his power of recollection? He did not know at first, and he does not know now, what is the side of a figure of eight feet: but then he thought that he knew, and answered confidently as if he knew, and had no difficulty; now he has a difficulty, and neither knows nor fancies that he knows.
Meno. True.
Socrates. Is he not better off in knowing his ignorance?
Meno. I think that he is.
Socrates. If we have made him doubt, and given him the "torpedo's shock," have we done him any harm?
Meno. I think not.
Socrates. We have certainly, as would seem, assisted him in some degree to the discovery of the truth; and now he will wish to remedy his ignorance, but then he would have been ready to tell all the world again and again that the double space should have a double side.
Meno. True.
Socrates. But do you suppose that he would ever have enquired into or learned what he fancied that he knew, though he was really ignorant of it, until he had fallen into perplexity under the idea that he did not know, and had desired to know?
Meno. I think not, Socrates.
Socrates. Then he was the better for the torpedo's touch?
Meno. I think so.

After these detours, Socrates uses the diagonal dissection of the square to arrive, with the slave boy, at the true belief:

Socrates. Mark now the farther development. I shall only ask him, and not teach him, and he shall share the enquiry with me: and do you watch and see if you find me telling or explaining anything to him, instead of eliciting his opinion. Tell me, boy, is not this a square of four feet which I have drawn?
Boy. Yes.
Socrates. And now I add another square equal to the former one?
Boy. Yes.
Socrates. And a third, which is equal to either of them?
Boy. Yes.
Socrates. Suppose that we fill up the vacant corner?
Boy. Very good.
Socrates. Here, then, there are four equal spaces?
Boy. Yes.
Socrates. And how many times larger is this space than this other?
Boy. Four times.
Socrates. But it ought to have been twice only, as you will remember.
Boy. True.
Socrates. And does not this line, reaching from corner to corner, bisect each of these spaces?
Boy. Yes.
Socrates. And are there not here four equal lines which contain this space?
Boy. There are.
Socrates. Look and see how much this space is.
Boy. I do not understand.
Socrates. Has not each interior line cut off half of the four spaces?
Boy. Yes.
Socrates. And how many spaces are there in this section?
Boy. Four.
Socrates. And how many in this?
Boy. Two.
Socrates. And four is how many times two?
Boy. Twice.
Socrates. And this space is of how many feet?
Boy. Of eight feet.
Socrates. And from what line do you get this figure?
Boy. From this.
Socrates. That is, from the line which extends from corner to corner of the figure of four feet?
Boy. Yes.
Socrates. And that is the line which the learned call the diagonal. And if this is the proper name, then you, Meno's slave, are prepared to affirm that the double space is the square of the diagonal?
Boy. Certainly, Socrates.

Socrates ends with the description of the process of knowledge:

Socrates. What do you say of him, Meno? Were not all these answers given out of his own head?
Meno. Yes, they were all his own.
Socrates. And yet, as we were just now saying, he did not know?
Meno. True.
Socrates. But still he had in him those notions of his-had he not?
Meno. Yes.
Socrates. Then he who does not know may still have true notions of that which he does not know?
Meno. He has.
Socrates.And at present these notions have just been stirred up in him, as in a dream; but if he were frequently asked the same questions, in different forms, he would know as well as any one at last?
Meno. I dare say.
Socrates. Without any one teaching him he will recover his knowledge for himself, if he is only asked questions?
Meno. Yes.
Socrates. And this spontaneous recovery of knowledge in him is recollection?
Meno. True.
Socrates. And this knowledge which he now has must he not either have acquired or always possessed?
Meno. Yes.
Socrates. But if he always possessed this knowledge he would always have known; or if he has acquired the knowledge he could not have acquired it in this life, unless he has been taught geometry; for he may be made to do the same with all geometry and every other branch of knowledge. Now, has any one ever taught him all this? You must know about him, if, as you say, he was born and bred in your house.
Meno. And I am certain that no one ever did teach him.
Socrates. And yet he has the knowledge?
Meno. The fact, Socrates, is undeniable.
Socrates. But if he did not acquire the knowledge in this life, then he must have had and learned it at some other time?
Meno. Clearly he must.
Socrates. Which must have been the time when he was not a man?
Meno. Yes.
Socrates. And if there have been always true thoughts in him, both at the time when he was and was not a man, which only need to be awakened into knowledge by putting questions to him, his soul must have always possessed this knowledge, for he always either was or was not a man?
Meno. Obviously.
Socrates. And if the truth of all things always existed in the soul, then the soul is immortal. Wherefore be of good cheer, and try to recollect what you do not know, or rather what you do not remember.
Meno. I feel, somehow, that I like what you are saying.
Socrates. And I, Meno, like what I am saying. Some things I have said of which I am not altogether confident. But that we shall be better and braver and less helpless if we think that we ought to enquire, than we should have been if we indulged in the idle fancy that there was no knowing and no use in seeking to know what we do not know;-that is a theme upon which I am ready to fight, in word and deed, to the utmost of my power.
Meno. There again, Socrates, your words seem to meexcellent.

In cconclusion, geometric dissections must have been familiar at least to the main thinkers of ancient Greece.

Alhabra Palace

[more from Frederickson]