return to the Geometric Dissections menu

Archimedes’ Stomachion

The oldest known mathematical puzzle dates from Archimedes, more than two millennia ago. It is, in fact, a dissection puzzle - and appears in a treaty known today as Archimedes’ Stomachion (or Ostomachion, or Syntemachion), contained in a Palimpsest written over by an anonymous medieval scribe compiling prayers. (The word palimpsest literally meant, in Greek, “scraped again”).

Apparently, Archimedes described in detail, piece by piece, a dissection of a square into 14 pieces: [1]

and asked how many different arrangements are possible. Aristotle’s original Greek text is available online, as well as an early 20th century Latin translation.

Here is the same solution, presented as a reflection of the previous one: [2]

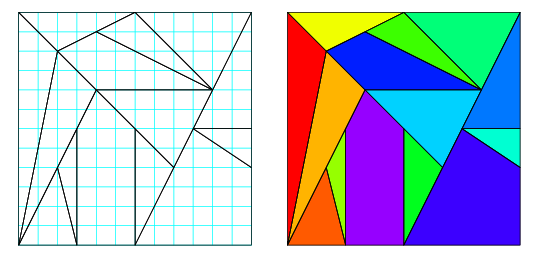
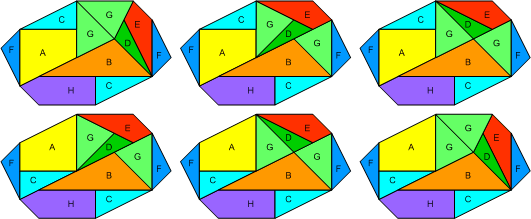
This problem of computational geometry was only recently solved—as it happens, by a mathematician with a doctorate in mathematics from Cornell University, Bill Cutler. Cutler showed that there are a total of 17,152 solutions, but some can be considered equivalent if a rotation or a reflecttion are performed. Cutler showed thaat Archimedes’ puzzle has exactly 536 truly distinct solutions [3], as follows: [4]

The dissection underlined on the sixth line is the one most often presented in discussions of Archimedes’ Stomachion: [5]

Let’s examine this pattern by measuring each polygon’s area: [6]

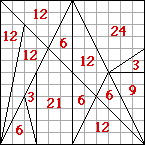
Simplifying by the common divisor 3, we obtain the following picture: [7]

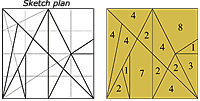
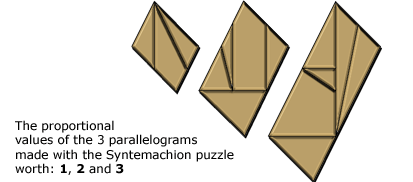
This makes obvious that the area of each piece in Archimedes’ puzzle is a multiple of 1/48 of the area of the whole square. A separation of the pieces and a convenient rearrangement shows that simple fractions of areas can be constructed using the pieces of the Stomachion: [8]

Many other shapes can be formed using Archimedes’ Stomachion pieces, including these: [9]

The following PDF file is a good starting point for a classroom activity related to the Stomachion, available from the National Council of Teachers of Mathematics: [10]

http://illuminations.nctm.org/Lessons/Stomachion/Stomachion-AS-ArchPuzzle.pdf

Further polygons can be constructed using all or some of the pieces in Archimedes’ problem, for instance these diamond-shaped decagons: [11]

ENDNOTES: