return to the Geometric Dissections menu

3-Dimensional (Polyhedral) Dissections

Similar to the definition for plane dissection, in three dimensions we call dissection of a solid a partition of it by planes. The resulting solid pieces of the decomposition can eventually be rearranged (with no intersections except plane surfaces) to obtain other solids, equivalent by dissection to the initial polyhedron and having the same volume.

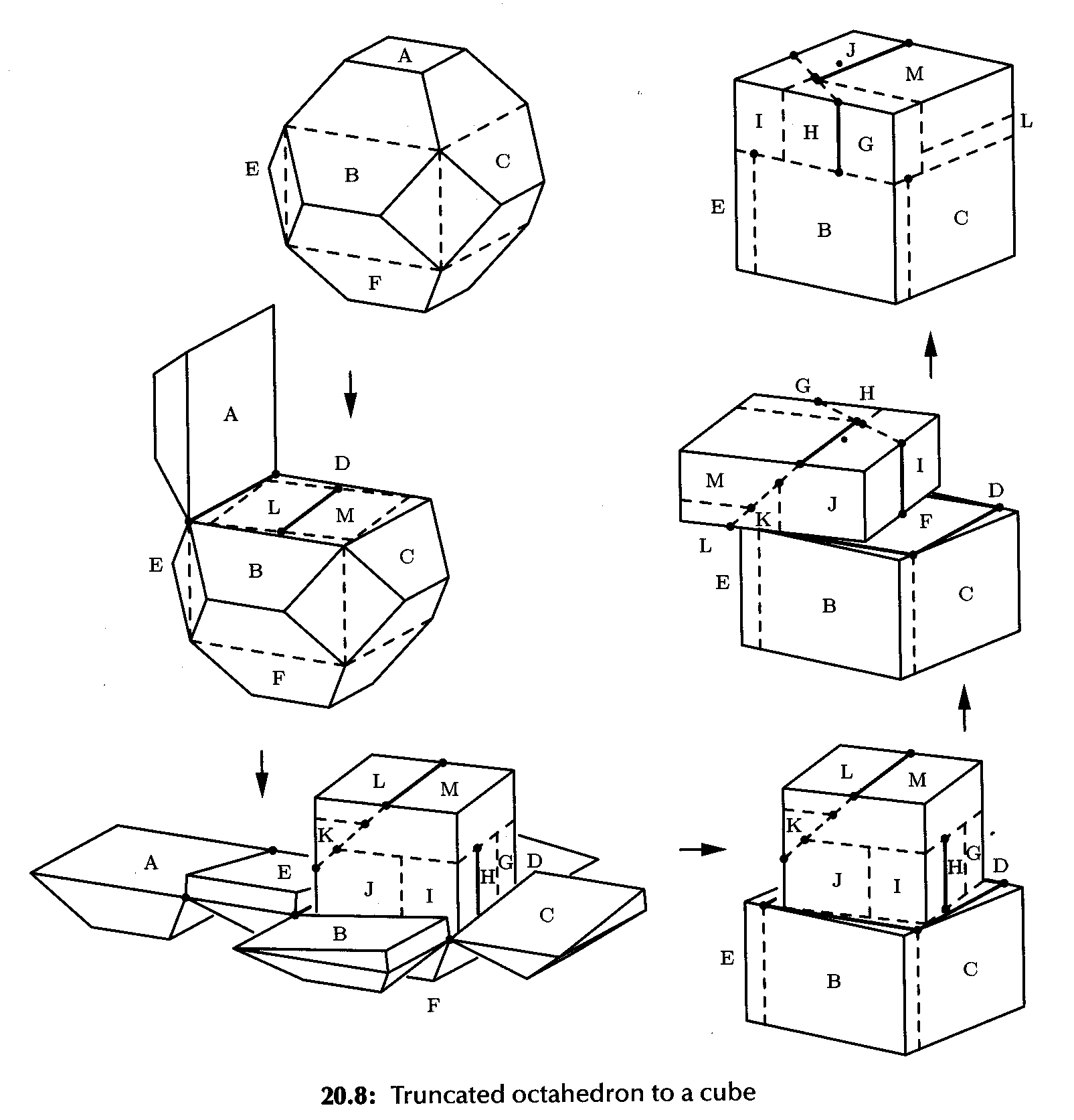
Greg Frederickson [1] reviews the existing literature on 3-dimensional dissections and gives some examples, starting with the hinged dissection of a rectangular block to a cube:

and continuing with several others, including the following:

Three dimensional dissections are hard to study systematically, due to difficulties in visualizing the objects obtained by cuts and imagining their arrangements. Nevertheless, work on 3-dimensional dissections is expanding - and so is the literature on it. The Rubik cube revolution during the last quarter of a century was part of a growing interest in solid dissections but the applicative potential of 3-dimmensional dissections is still enormous and little explored methodically, as of yet.

Three-dimensional dissections are essential in spatial puzzles.[2] Although not all dismembering of spatial objects used in puzzle making abide by the definition given above (since the pieces are not always convex), I present here several leads, to suggest possible paths for instruction and research. All the figures that follow are borrowed from Stewart Coffin’s excellent book The Puzzling World of Polyhedral Dissections.

A solid with the appearance of four mutually intersecting hexagonal prisms, together with triangular sticks who come from yet another hexagonal prism, can be decomposed in pieces which, reassembled, combine in a geometrical solid that appears to be made of four mutually intersecting hexagonal prisms:

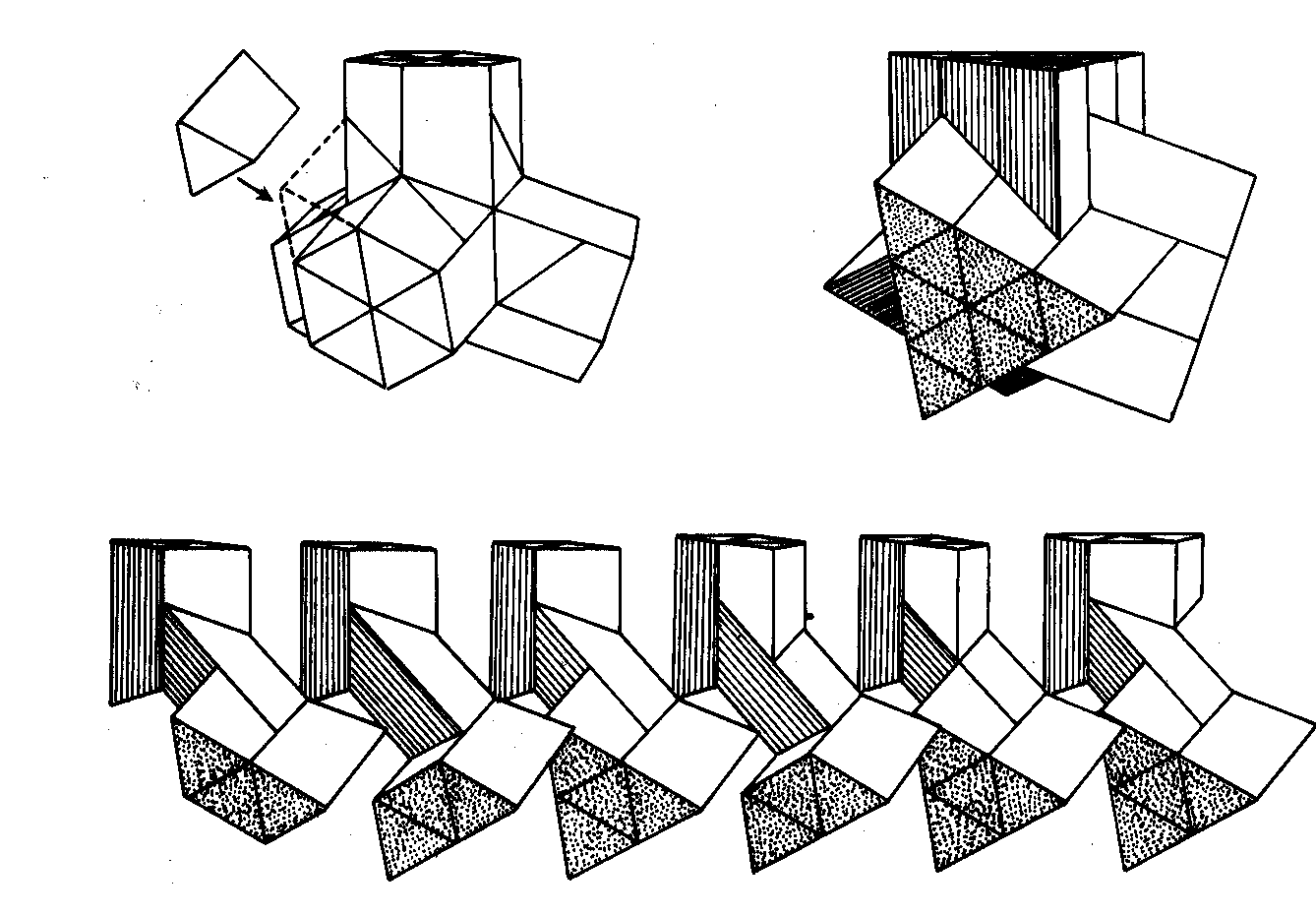
Additional triangular sticks can lead to the following solid:

having the appearance of four mutually intersecting stellar prisms.

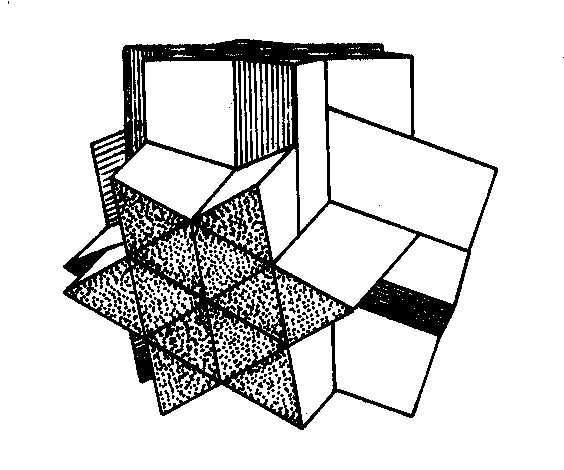
Extending the prisms in opposite direction (rather than building them up laterally) leads to objects like this one:

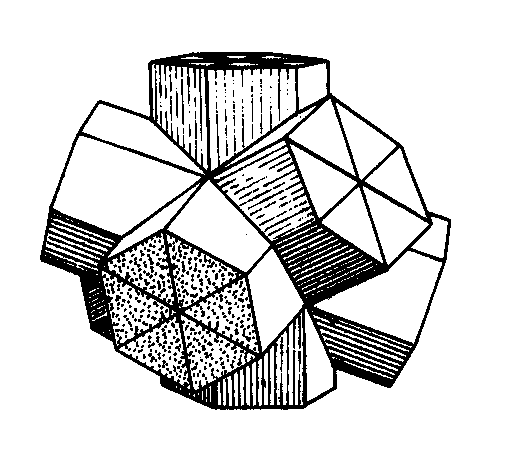
or this:

A rhombic dodecahedron can be dissected into nine pieces, like in the figure bellow:

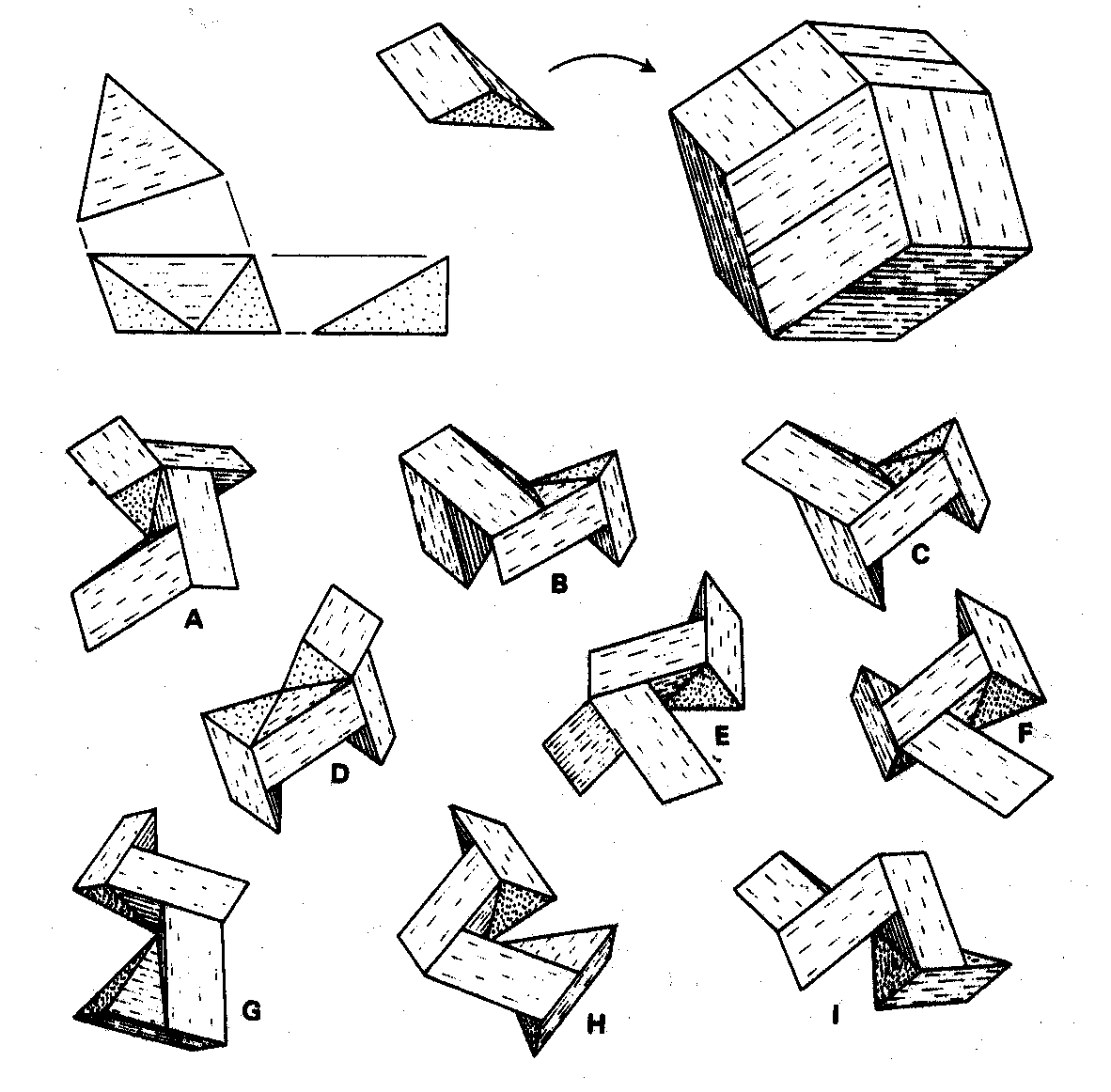
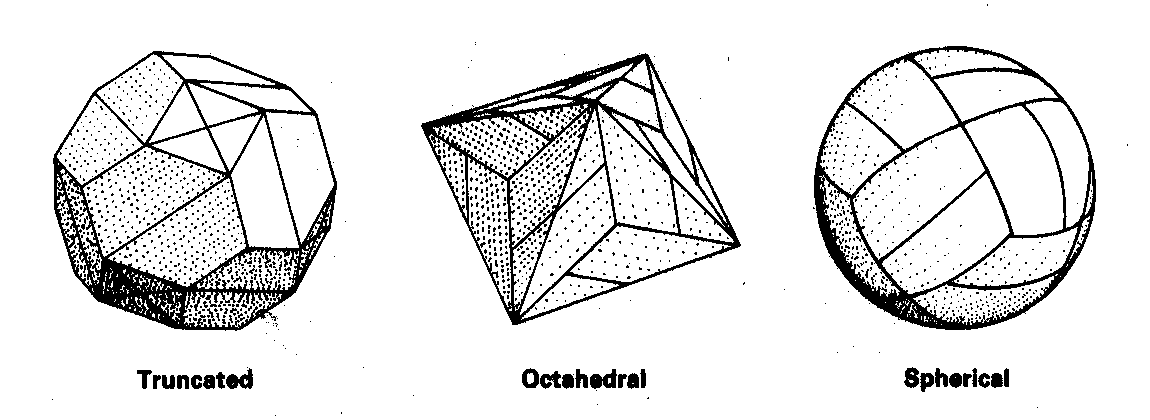
Coffin observes that the planes of dissection for the pieces above pass through the center of the rhomboid. Therefore, by truncating the fully assembled dodecahedra we can obtain any of the following shapes:

ENDNOTES: