The set of points which are equally far from p_1 as they are from p_2 is a plane which is sandwiched on either side by the points, p_1 and p_2.
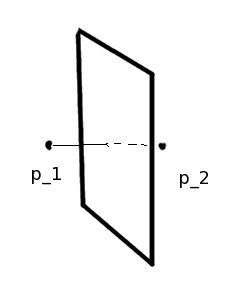
Next, pick a third point, and notice that it will not do to pick a point that is in the line connecting p_1 and p_2. Call this point p_3. Now that we have 3 points, again we ask, what is the shape describing the set of points in 3 space equally far from each of 3 non-colinear (i.e., not in a line) points. If you didn't understand the last one, but you've seen the answer, go ahead and try to work this one out, it's entirely analogous.


