Maybe not an easy question. We will prove that in fact this is the entire list.
The first observation is that each corner looks like a pyramid (of various numbers of edges coming together) and if we allow ourselves to cut along one edge we can lay one corner out flat, whereby the pyramid becomes a shape in the plane which appears to be _missing a piece_
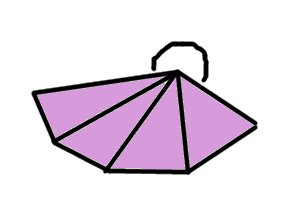
It will therefore be argued that the sum of the angles of the polygons around a corner will add up to strictly less than 360 degrees. Suppose there are k faces meeting at a point, and each face is a n-gon. Then by our previous work, the sum of the angles of the polygons around one corner will be
k*(180*(n-2)/n)
and we have
k*(180*(n-2)/n)=k*(180-360/n)<360
Can k be very large? If not, how large can it be?


