To really talk about this problem requires a little background - to start, we’re gonna discuss some things we’ll take as facts about spheres, because even though they CAN be proved, it would take more time than we have here.

Let’s start by drawing a sphere and picking a point on it:

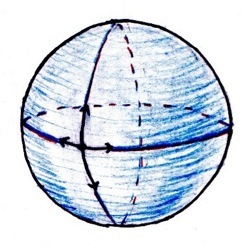
If we imagine this as the earth, with 360 degrees around the equator and 360 degrees along the central latitude line, we pick a point and rotate it some irrational number of degrees around the equator.  Let’s call this irrational number A.  We will rotate that point some number of times - as many as we want.  Next we pick another irrational number B.  We will rotate our point some number of times, B degrees, at a right angle to our original rotation.  We keep doing this, rotating A or B degrees in one direction or the other, always at right angles to one another.

That means the word ABBBBBBBB is the same as the word A, for example!

Fact 3 is pretty straightforward - we could have started with any point, since the sphere looks “just the same” no matter how you rotate it!

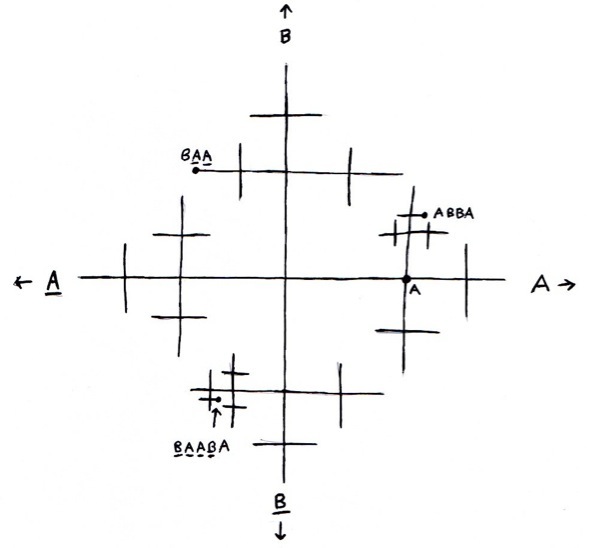
Basically, we are going to group together sets of points where two points are in the same set if we can get from one to the other doing some series of rotations at angle A, A, B, or B.  So looking at our Cayley graph above, we see that the point at the center is in the same set as the point represented by A, along with the point that we would get to by rotating BAABA, or BAA, etc.

The reason this rates quotation marks around “fact” is that it’s NOT obviously true we can do this.  If there were finitely many (or countably many!) of these, we could easily do it - but for an uncountable set of sets, it’s actually impossible to prove whether we can pick one from each or not.  If we accept that we can as a fact, the rest of the Banach-Tarski paradox is going to follow!

Now that we have all of that done, let’s lay out how the paradox works!

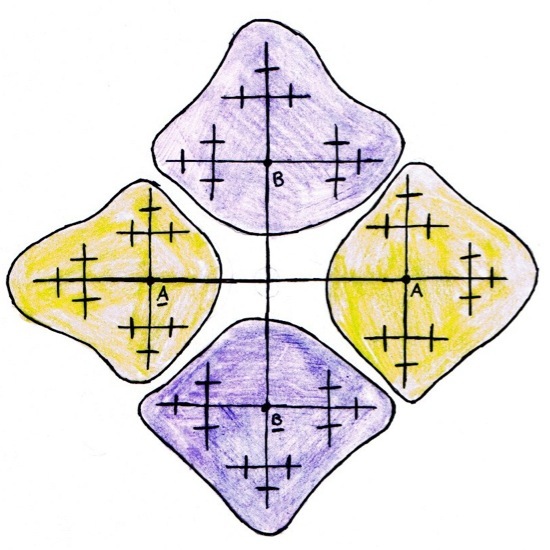
Looking at this picture, we see that we can break up each of these Cayley graphs in to five pieces - the center, the top and bottom purple pieces, and the left and right green pieces.  All of the points corresponding to the center are the representatives that we picked, by the way.

Now we get down to more serious business.  Let’s just look at the top purple piece now.  You should notice that in the next picture, we’ve drawn the top purple piece in a little more detail, adding one extra letter to each of our words.  Looking closely, we see that the top purple piece “looks the same” as the top purple piece and the two green pieces put together!

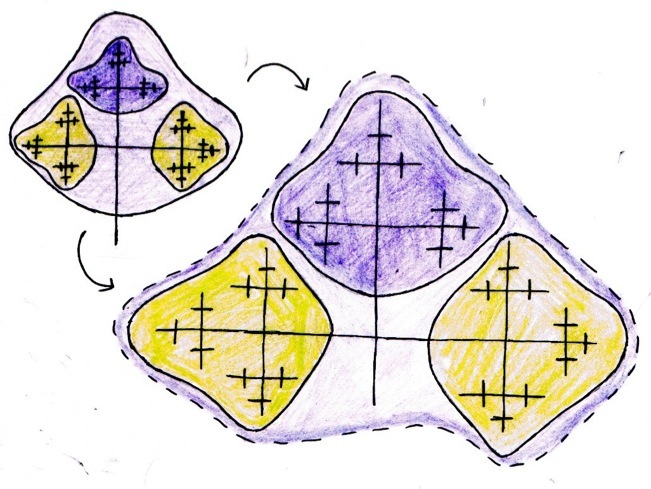
If we wanted to rigorously define our map that takes us from the small top purple pieces to the top purple piece and the TWO green pieces, we need to go back to how we characterized the top purple piece.  If you did Exercise 2, you probably realized that the top purple piece is made up of all words starting with the letter B and the bottom piece is made up of all words starting with the letter B.  We are assuming that all of the words are in “reduced form,” so if they start with B, the next letter isn’t B, and similarly, if they start with B, the next letter wasn’t B.

If we take each of the words in that top purple part and remove the first letter, we can get ANY word in the top purple or the left and right green pieces!

We could have done EXACTLY the same thing looking at the right green piece and removing the first letter A from each of those words.  So looking at a (much rougher) picture of our Cayley graph, we see that we could take the top and bottom purple piece, “stretch” out the top purple piece to cover the whole top three quarters, and get our WHOLE set back.  In the diagram below, you can see how we could do the same for the right green piece - and with that, we have broken our set up in to five pieces, taken four of them and reassembled them into two full sized copies of our original set, and we throw away all of our extra “center pieces.”

What does having two full sized copies of our original set really mean?

We now have two full sized spheres the SAME size as our original sphere, even throwing away a LOT of points.  We just chopped our sphere up into four pieces, rotated two of the pieces (because that’s all removing A or B from the words is doing to the actual points, by the way,) and stuck them back together to make two sets that sum up to twice the size of our original.

We rotated our sets, and made them bigger!  This crazy reassembly is called the Banach-Tarski Paradox!  That’s also the joke in the title of this page:

Mathematician 1:  “What an anagram of Banach-Tarski?”

Mathematician 2:  “Banach-Tarski, Banach-Tarski.”

<<Back to Main>>