This problem is a nifty question about infinity - but before looking at the answer, think about it for a while!

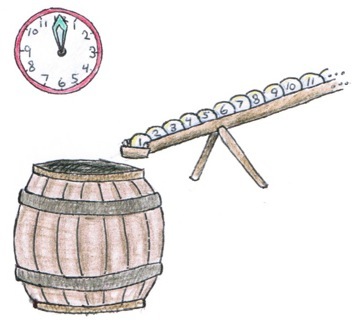
Let’s say we have a giant barrel - and by “giant,” I mean of infinite size, so it can hold absolutely as much as we want.  Above that barrel, angling down from way on high, we have a long chute with a little gate at the end above the barrel, and from that gate to as far away as we can see lies a row of tennis balls.  Each of those balls, all sitting nicely in that line, have a number painted on their side.  Conveniently, they’ve been lined up in order - ball 1, followed by ball 2, followed by ball 3, all in order as far as the eye can see.

On the wall behind the chute and barrel, there is a clock.  We wait for the clock to strike midnight then get ourselves ready - it’ll be a busy hour ahead.  At 30 minutes after the hour, we open the gate to allow 10 balls to drop in to the barrel.  In the same motion, we grab the 1st ball, and pull it out of the barrel and throw it away.

At 45 minutes after the hour, we open the gate, drop 10 more balls in, and in the same motion, fish out ball number 2 and throw it away.  We continue doing this - when the clock hits halfway from our last ball drop until 1 am, we drop in ten more balls and pull out the next numbered ball that we haven’t removed already.  At any given moment, there are nine times as many balls still in the barrel as we have pulled out.  We keep doing this, faster and faster and faster (eventually, we’re doing this many times a nano-second as we get quite close to 1!)

This isn’t as obvious as it first appears.  At any given instant, you’ve dropped nine times as many balls into the barrel as you’ve pulled out, and it looks like the barrel is getting more and more filled with balls.  However, think about any particular ball you like - whether it is 9 or 10,000,000.  Will it be in there when the clock strikes 1?  Why or why not?

After you’ve tried the problem for a while, go check out the answer page.  Next try a different version of the problem:

We set up our clock, chute, and barrel all over again.  Now, when the clock strikes 30 minutes after the hour, we drop balls 1 through 10 in and fish out ball #10.  Fifteen minutes later, we drop in balls 11 through 20 and fish out ball #20.  We continue this way at each halfway mark until the hour, dropping in ten more balls and fishing out the last one.  Now we ask our question again!

Uh, oh.  That didn’t work out the same way.  Think about it for a bit, then one more question.

We do this all over again.  This time though, our chute is different - instead of the balls being labelled, we just have plain tennis balls without any markings at all.  At each halfway point to the hour, we drop in ten balls, just like before - but this time, when we fish out a ball, we just pick randomly from all of the balls in the bin.  As a final question then:

<<Back to Main>>