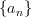satisfies 
for some integer m, with d being the leading digit we choose.
Recall that we want to find the what proportion of a sequence 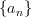satisfies for some integer m, with d being the leading digit we choose.
Let's go over our example of population growth and modify things to give a new interpretation: the probability becomes
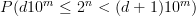
Call the last equation (1).
Interpretation: Note that log d and log (d+1) lie between 0 and 1, so even though we specify m is whatever integer, it is forced to be the greatest integer that's less than $latex n\log 2$ (for example if n log 2=23.134... m has to be 23 and n log 2-m = 0.134...). Notation: n log 2-m will be denoted n log 2 mod 1 and geometrically the interval from 0 to 1 is glued to become a circle and 0.3 is the same as 1.3, 2.3, ... and as n increases by 1, n log 2 mod 1 looks like rotation around a circle (with an irrational angle of 108.37... degree). Hence the name irrational rotation, meaning log 2 is irrational (Exercise: why is log 2 irrational? hint).
Notice the answer we seek (log(d+1)- log d) is precisely the difference between the left and right bound in 
. So what we need to see is that the sequence of points generated by irrational rotation is evenly distributed around the circle:
Definition: 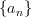is equidistributed in [0,1] if for any interval (a, b) in [0,1], the proportion of 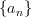in (a, b) is b-a.
So we are done if we show n log 2 mod 1} is equidistributed. [0,1] means the interval from 0 to 1 including 0 and 1.
By the way, if we repeat everything above replacing {2^n} by 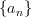, we get the following:
Sufficient condition for Benford: if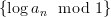 
is equidistributed in [0,1], then 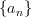is Benford.
In fact this is how many sequences are shown to be Benford.
Example 1: showing geometric Brownian motion is Benford is reduced to showing bell-shape probability distribution mod 1 is equidistributed in [0,1], which is more tractable although still messy. Therefore we won't do it (showing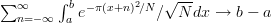 
as N approaches infinity).
Example 2: Fibonacci sequence is Benford. It is defined by recurrence relation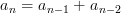 
and the first two values are 0 and 1. In fact, most sequences defined by recurrence relation is Benford. The reason is that they are roughly exponential (for Fibonacci, 
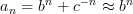where b, c>1), so that taking log gives something that looks like irrational rotation for large n and can be shown to be equidistributed.
(Details for these examples can be found here)
Let's get back to showing Theorem: Irrational rotation, {n b mod 1}, is equidistributed in [0,1], where n=1, 2, ... and b is irrational (Exercise: what happens if b is rational, say 3/4?)
One thing special about irrational is the following
Property: For any x in [0,1], there exist some number in {n b mod 1} as close to x as we want (but not equal to x). Proof by example: let's say x=0, b=0.31 and we want to find n so that n b mod 1 so that we get closer to x by half or .31.../2. From the sequence {0.31..., 0.62..., 0.93...=0.07..., ...}, it is not hard as the third number is good enough . It turns out we can keep on repeating, this time getting closer than .07.../2: {.07..., 0.14..., ..., .98...=0.01...}. So why does it work? Because as you get close to x, the two numbers in the sequence that sandwich x are distance b away from each other so one of the two numbers has to be at most b/2 away from x. Picking x to be 0, we have find a way to increment be less than b/2, and so we have find a way to continue, this time finding two numbers in the sequence separated by less than b/2 that sandwich x (why doesn't this work for rational, say b=1/4? It fails during the second step using x=0, because some points land on 0 and so we cannot cut the distance from x by half.)
Going back to the theorem, we want to see why it works for the case [0, 0.5]. We need to show the proportion*
as n approaches infinity.
Proof (Sketchy): It looks nasty to compute so let's be crafty. We can ask about the proportion for [0.5, 1] instead. The answer should be the same intuitively and the above property confirms our intuition: by skipping an initial segment of {n b mod 1}, it will be {x+ n b mod 1} for any x arbitrarily close to what we want, which is 0.5. Although skipping an initial segment will affect the proportion, but letting n go to infinity eliminates the effect. Finally, since the proportion in [0, 0.5] and [0.5, 1] must add up to 1, each must be 0.5 and we are done. This argument can be repeated for other intervals and we are finally done.
The above concept is called translation invariance, characterizing uniform probability uniquely and is thus useful in proofs. It will be seen later because it is a disguise for scale invariance of log distribution.
Exercise a (generalized Benford's law): If instead of the leading digit, we specify the first two digits that we want the probability, say what's the proportion of 2^n with starting with 14, how would you compute it? Can you come up with a general formula? How about if we use base 7 instead of base 10.
Answer: You want to repeat the procedure to get (1). The first one is log 15 - log 14. If you change the base, then again repeat and you will see that the formula only changes from log base 10 to log base 7.
Different View: Dynamical System The proportion* above is called the time average as you think of the irrational rotation as happening every second. There is also a space average, which is just the length of the interval under consideration (for above it was [0, 0.5]). Equidistribution can be obtained without using the sketchy argument above: it is a consequence of the fact that time average equals space average:
where Tx=x+b, and f(x)=1 if x mod 1 is in the interval ([0, 0.5] for above) and f(x)=0 otherwise.
Exercise: how does this give equidistribution?
For those who know fourier series, the proof of the formula with our specific map T involves showing the formula is true for f(x)= cos(2 pi n x)$ (or sine) and then claim that we are done because f is periodic.
For more detail, click here.
Next: scale-invariance or if you are tired, go Home