Benford's Law

This article will explore a pattern that occurs in a variety of random samples of data, such as sizes of counties and populations, physical constants like densities and molecular masses, stock prices and as random as numbers appearing in newspaper. We want to study the distribution of the left-most nonzero digit (ranging from 1 to 9), also called the leading digit. At first thought, each value seems to have equal probability (=1/9). But it turns out 1 is much more likely to be the leading digit than 9. Exact probabilities are shown in the chart below.

Several possible explanations include:

1. Upper bound: How would you obtain data with leading digits evenly distributed among 1 to 9? One way is to use a random number generator from 1 to 99. This requires us to specify an upper bound but naturally occurring data does not have such a bound (the lower bound will always be 0 since we are concerned with positive numbers only). Also the upper bound has to be 9 or 99 or 999 ... for 1 to 9 to have the same probability; if the bounds is 1 and 19, then the leading digit will more likely be 1.

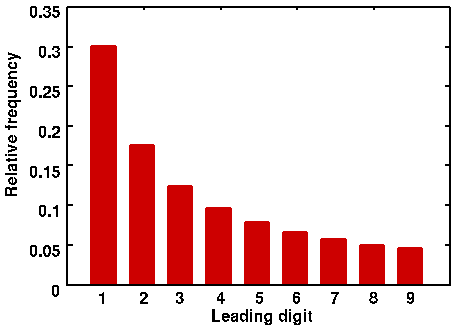
   With this explanation, certain examples, such as numbers in the newspaper, following this distribution seem to make more sense. To understand how to get the exact probability try the following Exercise.

2. Exponential: population over time is roughly exponential. Suppose it starts at 1 and doubles every year (P(t)= 2^t), then it takes 1 year to go from 1 to 2. To reach 3, solve 2^t=3 using a calculator, we get t=log 3/log 2= 1.585..., so it takes only 0.585 years to go from 2 to 3. This will continue to decrease because of exponential growth. But it will jump up when you calculate the time spent at 10 to 20 because we increased the increment when we go from unit digit to tens.

   Exercise 2: calculate the time spent from 10 to 20. Using properties of logarithm, what can you conclude?

   From this exercise, you can kind of see the fraction of time spent from 1 to 2, 10-20, 100-200, ... versus the total time is just the fraction of time spent from 1 to 2 versus 1 to 10. Using properties of log, the answer is log 2 =0.301.... This is exactly the one appearing in the above graph.With this calculation we obtain the log distribution: probability that the leading digit is d equals log(d+1)-log(d)=log (1+1/d).

   Definition: A sequence of numbers 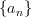is Benford if the leading digits approaching the log distribution in the limit as n approches infinity.

   It is sometimes simpler to work with the probability that the leading digit is d or less because it is log(d+1). To understand why many phenomena satisfy Benford's law without being exponential require us to explore exercise 2 more rigorously.

3. Multiplicative (Geometric): It turns out that lots of phenomena that are multiplicative in nature can be shown to satisfy Benford's law. The way it is proved is similar to exponential growth. From log ab = log a + log b, we can reduce multiplicative processes to linear ones, which is usually easier. For example, the stock market can be modeled by multiplying it by 2 and 1/2 with probability .5 and .5 , respectively, every year (where the values given are arbitrary and certainly inaccurate). If we take log, this becomes adding 1 and -1 with probability .5 and .5, which is like flipping a coin and trying to figure out the total number of heads after some time (the latter is called random walk and can be modeled by a bell-shaped curve by the Central Limit Theorem; the former is called geometric Brownian motion (illustrated below) and satisfies Benford's law)

   
4. Universal: Forget about the previous explanations. If there is a law about leading digit of physical data, then it shouldn't depend on what unit; if it works for stock prices in US dollar, it should also work for Euro or British Pound. This is called scale-invariance. With this idea in mind, we will see that log distribution satisfies this property. More importantly, it is the only distribution that satisfies the probability.

   To give a definition of scale-invariance, we start with a sequence 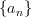with the probability that a number from the sequence has leading digit less than d denoted by D(d), then this probability will be the same as that of the sequence 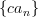, for any c>0.

   Similarly we can change the number system we use: instead of base 10, we use base 8. We hope this will again give us log is the only distribution that work (this won't work though because the sequence {1, 1, 1, ...} is the same no matter what base we are in. That means the distribution with 1 being 1 and everything else 0 will screw things up. But that's the only problem.)

Next: upper bound or if you are tired, go Home