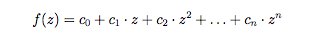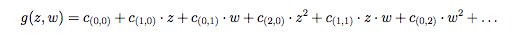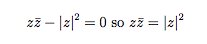
and therefore
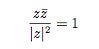
Set
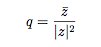 .
.
Finally, we define
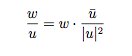 for any non zero w,u.
for any non zero w,u.
Polynomials in complex variables.
It turns out that complex numbers are extremely useful in many problems in engineering and physics, especially in areas of electrical engineering, optics, and acoustics, and it has become a huge field in its own right in mathematics. Some of the simplest functions, that are quite easy to define, are the polynomials, which are defined just as in the real case. We have addition and multiplication already, as well as scaling by a real number, so we will define a complex polynomial of one variable to be a an expression
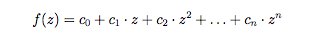
where the c_i's are each complex numbers. Here you can plug in any complex number z and f will give you a complex number back, the value of f at z.
If we allow more input variables, say z,w, we can write
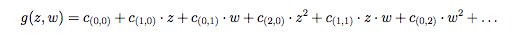
(can you see the pattern here?)
Then plugging in two complex values to g, we get one complex value back, the value of g at (z,w) (remember each of these is complex, so this pair represents two points in the plane).
If you've studied calculus you know about limits and continuity, derivatives, power series and integrals. All of these extend with little effort to complex numbers, as well as exponential and logarithmic functions, and many topics become much clearer when extended to complex numbers, such as the relationships between hyperbolic trigonometric functions sinh, cosh, tanh, and their trigonometric counterparts sin, cos, tan. There is far too much to say, but we have enough foundation to apply to an interesting problem involving linkages.
You can also return to the table of contents,
or back to the MEC home page
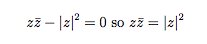
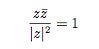
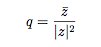 .
.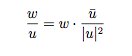 for any non zero w,u.
for any non zero w,u.