In fact the pantograph will do both of these! If we anchor the pantograph with its lower middle vertex fixed to 0 we get a linkage where two points oppose each other as reflections through the origin.



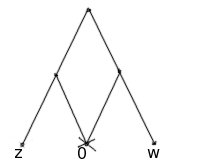
Can you see how w is always -z? We can also use the pantograph to half a complex number.



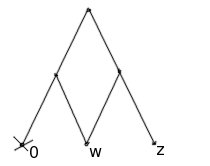
This is our original pantograph, just with input and output switched.

Next, we'll keep building on what we already have. We need a way to add 2 numbers. How can we make a linkage that will take two numbers as input and give their sum as output?

Hint: first find a way for getting the average of two complex numbers.