|
5. Hyperbolic GeometryHyperbolic geometry is the geometry you get by assuming all the postulates of Euclid, except the fifth one, which is replaced by its negation.
In hyperbolic geometry there exist a line
It is more difficult to imagine, but have in mind the following image (and imagine that the lines never meet
The first property that we get from this axiom is the following lemma (we omit the proof, which is a bit technical):
Lemma 1
Rectangles don't exist in hyperbolic geometry.
Using this lemma, we can prove the following Universal Hyperbolic Theorem:
Theorem 1
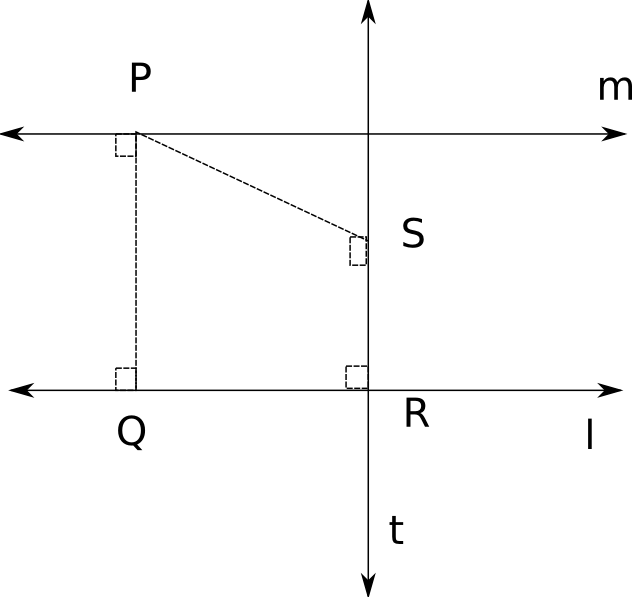
In hyperbolic geometry, for every line
PROOF.
Drop the perpendicular
Let
Assume that
Theorem 2
In hyperbolic geometry, all triangles have angle sum
Theorem 3
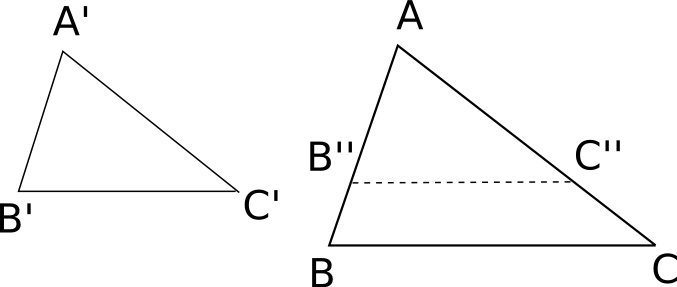
In hyperbolic geometry if two triangles are similar, they are congruent.
Note: This is totally different than in the Euclidean case. It tells us that it is impossible to magnify or shrink a triangle without distortion.
Assume the contrary: there are triangles
Then, by definition of
But we also have that
Hence similar triangles are congruent.
An amazing consequence of this theorem is that in hyperbolic geometry a segment can be determined with the aid of an angle. This is stated more dramatically by saying that hyperbolic geometry has an absolute unit of length!
Defect and area of a triangleThere is also the concept of the defect of a triangle, which is defined to be the quantity that is missing for the sum of the angles to add up to 180 degrees. And in fact the area of a triangle in hyperbolic geometry is proportional to its defect D. So we have that A=kD, where k is a positive number.Two triangles have the same area if and only if they have the same angle-sum.
Now that you have experienced a flavour of proofs in hyperbolic geometry, Try some exercises!
ExercisesThe following are exercises in hyperbolic geometry. You are to assume the hyperbolic axiom and the theorems above.
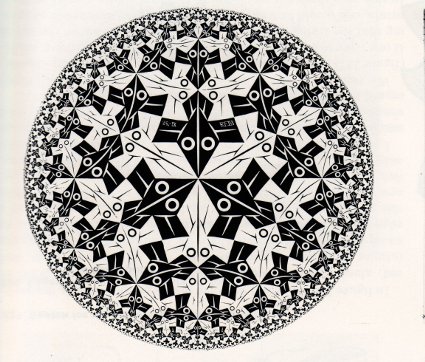
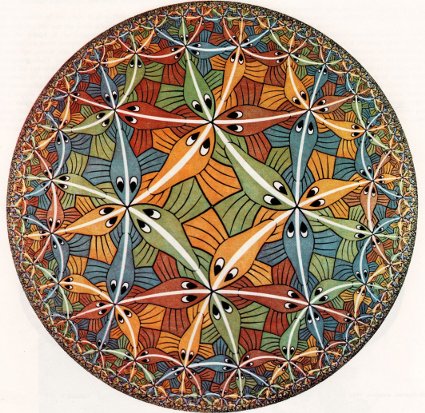
Back to EscherM. C. Escher created four patterns using hyperbolic geometry: Circle Limit I, Circle Limit III, Circle Limit III and Circle Limit IV. What Escher used for his drawings is the Poincaré model for hyperbolic geometry.
What does it mean a model? By a model, we mean a choice of an underlying space, together with a choice of how to represent basic geometric objects, such as points and lines, in this underlying space. The need to have models for the hyperbolic plane (or better said, the hyperbolic geometry of the plane) is that it is very difficult to work with an Euclidean representation, but do non-Euclidean geometry. As you saw above, it is difficult to picture the notions that we work with, even if the proofs follow logically from our assumptions. There are two more popular models for the hyperbolic plane: the upper half-plane model and the Poincaré plane model. We will analyse both of them in the following sections. |