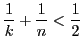9. Tesselations of the Euclidean and non-Euclidean plane

Definition 1   A plane tessellation is an infinite set of polygons fitting together to cover the whole plane just once, so that every side of the polygon belogs also to another polygon. No two of the polygons have common interior points.

We will analyse only regular tessellations.

Definition 2   A tessellation is called regular if its faces are regular and equal. The same number of polygons meet at each vertex. We denote with $ \{n,k\}$ (called a Schläfli symbol) a regular tessellation that consists of regular polygons with $ n$ sides and at each vertex $ k$ edges meet.

(There are also quasiregular tessellation - built from two kinds of regular polygons so that two of each meet at each vertex, alternately.)

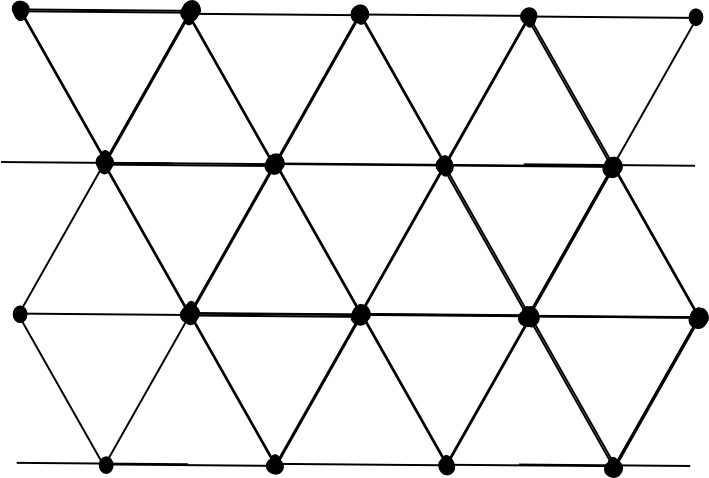
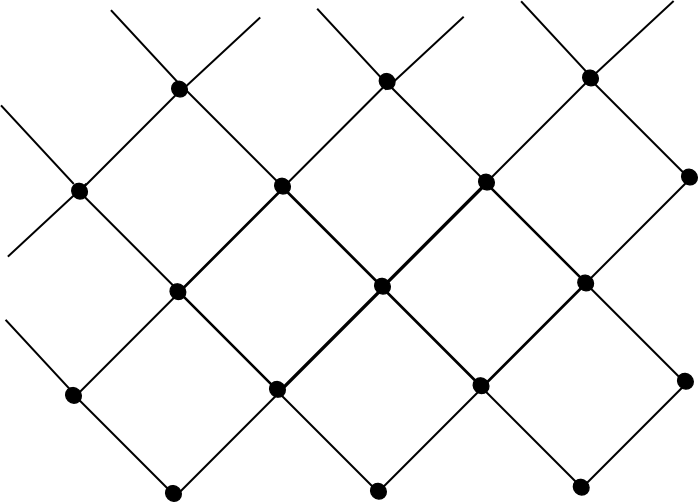
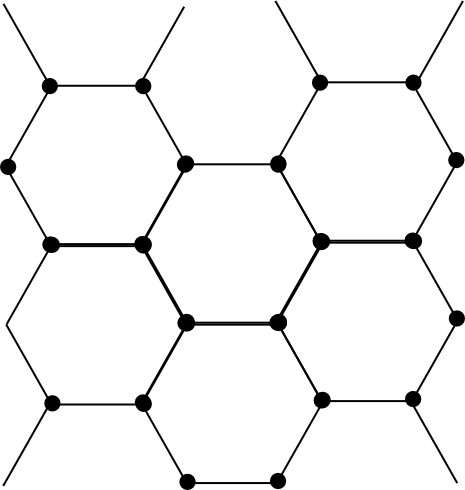
Regular tessellations of the Euclidean plane


In the Euclidean plane there are only 3 possible tessellations: $ \{3,6\}$ in which equilateral triangles meet six at each vertex; $ \{4,4\}$ in which squares meet four at each vertex; and $ \{6,3\}$ in which hexagons meet three at each vertex. Let's see why this is true.


The internal angle of a regular $ n$-polygon is given by the formula $ \pi\left(1-\frac{2}{n}\right)$. There are $ k$ edges that meet at each vertex, so there are $ k$ internal angles that add-up to $ 2\pi$. Hence we have:

$\displaystyle k\cdot\pi\left(1-\frac{2}{n}\right)=2\pi \Rightarrow \frac{2}{k}=1-\frac{2}{n} \Rightarrow \frac{1}{k}+\frac{1}{n}=\frac{1}{2}$ where $\displaystyle k,n\in\mathbb{N}$    

This equation has only 3 solutions: $ n=3, k=6$, $ n=4, k=4$ and $ n=6, n=3$. Here is how they look:


Image Section91 Image Section92 Image Section93
$ \{3,6\}$ $ \{4,4\}$ $ \{6,3\}$


Regular tessellations of the hyperbolic plane


There are infinitely many regular tessellations of the hyperbolic plane. Since in the hyperbolic plane, the sum of the angles of a triangle is less than $ 360^{\circ}$, it follows that by doing the same computation as above (just replace the fact that the $ k$ angles add up to something $ <2\pi$), we get:

$\displaystyle \frac{1}{k}+\frac{1}{n}<\frac{1}{2}$    

But this happens for infinitely many pairs of $ \{n,k\}$.


Here are some examples (thanks to http://aleph0.clarku.edu/~djoyce/poincare/poincare.html).

Remember that even if it may look like the sides of the pentagons are curved, they are not - the effect is due to the representation we're using. In the actual hyperbolic plane they would be straight. Also, the pentagon in the middle looks larger, but in fact it isn't. All the pentagons are absolutely identical (in the hyperbolic world).
{5,4}-tessellation
{4,5}-tessellation
Quasi-{5,4} tessellation
Quasi-{6,4} tessellation

We started with Escher, let's finish with Escher. Here are two "regular divisions of the plane" (that's the name Escher used for tessellations):

"Regular Division of the Plane III" (1957)
"Regular Division of the Plane IV" (1957)


INDEX
NEXT