Euler Characteristic

Suppose you're given some closed surface, like the one on the right. How can you tell which of the surfaces in the classification it's topologically equivalent to? One way is to try deforming it until you can make it look like an n-holed torus or a connected sum of projective planes. While in this case doing so isn't terribly difficult, in general it can be quite a puzzle. Yet there's another, much simpler method, relying on a single number. That number is the Euler characteristic of a surface.

The Magic Number

Calculating the Euler characteristic of a surface is traditionally done using a triangulation of that surface. A triangulation is just what it sounds like: the division of a surface into triangles in a "nice" way. Nice here means that the intersection of any two triangles is either a single point which is a vertex of each triangle or a single edge which is a side of each of the triangles. Here's an illustration. triangulation

Activity 1: Triangulate!

Why is the subdivision of the torus on the right not a triangulation?
What is the minimum number of triangles needed to triangulate a sphere?
Draw two different triangulations of the projective plane

The Euler characteristic is equal to the number of vertices minus the number of edges plus the number of triangles in a triangulation. Normally it's denoted by the Greek letter χ, chi (pronounced kai); algebraically, χ=v-e+f, where f stands for number of faces, in our case, triangles.

Activity 2: The χ of a surface

Consider the "good" triangulation of the sphere illustrated in the beginning of this section. What is Euler characteristic of this triangulation? (Hint: there are 6 edges.)
Calculate the χ of the two triangulations of the projective plane you found in the previous activity. (Hint: you should get the same number.)
Draw a donut-surface torus and find a triangulation of its surface. Calculate its χ. Is it equal to the χ of the "ugly" triangulation given in the beginning? (Hint: note that the vertices on the edges of the ugly torus triangulation are not all distinct!)

From the above activity you should notice a certain pattern: the Euler characteristic of two triangulations of the same surface is the same! This is a theorem, part of which we'll prove.

Triangles on a Sphere

Suppose we have a sphere of radius 1. Recall that the area of a sphere is equal to 4πr², so that our unit radius sphere has an area of 4π.

Activity 3: The area of a triangle

The following steps, coupled with the illustration below, will guide you in finding the area of a triangle on a sphere in terms of its angles.

What is the area between two great circles in terms of the angle x between them? (Hint: what's the total angle around the point of intersection, or any other point for that matter?)
Consider a triangle on the sphere with angles x, y and z. The great circles forming the triangle also form a triangle on the "other side" of the sphere. What are the angles of that triangle? What is its area in terms of the area of the original triangle on the side facing us?
Examine the areas I_x, I_y, I_z. Which points of the sphere are only in one of those sets? Which are in two? Which are in all three? (Hint: every point is in at least one of them.)
Use these results and the fact that the area of the whole sphere is 4π to express the area of the triangle in terms of x, y and z.

If everything went according to plan, you found that in fact 4π=4x+4y+4z-4A, where A is the area of the triangle, so that A=x+y+z-π. This confirms that, as we've seen in the last section, the angles of a triangle on a sphere add up to at least pi, since having negative area is impossible. How does this relate to the Euler characteristic? Let's find out.

Activity 4: Summing things up

Suppose we have a triangulation of the sphere. What is the number of edges in terms of the number of triangles (e in terms of f)? (Hint: each edge is part of two triangles.)
Use the expression you got for the area of a triangle to write the total area of the sphere in terms of the number of vertices v and the number of triangles f.

So you got 4π=2πv-πf. What now? Well, we would like to get the Euler characteristic χ=v-e+f in here, so why not add and subtract 3πf on the right, getting

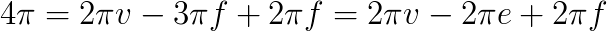
by part 1 in the activity above. Canceling 2π on both sides, we get
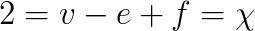
2=v-e+f=chi

Congratulations! We've just shown that no matter what triangulation you take, the Euler characteristic of a sphere is 2. Note that knowing that in a plane the sum of a triangle's angles is exactly π, we can apply the same analysis to our flat surfaces, the Torus and Klein bottle.

Activity 5: Fingerprinting the flat surfaces

Suppose we have a triangulation of a torus or a Klein bottle. What is the sum of all the angles in terms of the number of vertices v?
What is the sum of the angles in terms of the number of triangles f?
Write out the equality implied by the questions above and use the previous trick, add and subtract 2πf. What do you get for the Euler characteristic?

From the above you should see that the Euler characteristic of both the Klein bottle and the torus is 0.

Activity 6: Not forgotten

The projective plane, like the sphere, has spherical geometry. Modify our analysis of the sphere to find the Euler characteristic of the projective plane. (Hint: almost everything stays the same, except the projective plane has half the area of a sphere.)

Now we have all the tools needed to calculate the Euler characteristic of any surface!

Activity 7: The good ol' connected sum

Suppose we have two closed surfaces S₁ and S₂, with Euler characteristics χ₁ and χ₂ respectively. What is the Euler characteristic of S₁#S₂? (Hint: see the picture below. How many vertices, edges, and faces does the new triangulation have, in terms of the vertices, edges, and faces of the old ones?)
What is the Euler characteristic of a torus#torus? A torus#torus#torus?
What is the Euler characteristic of the connected sum of n projective planes?

We've done it! Now, simply knowing a surface's Euler characteristic, and whether it's oriented or not, we can tell what it is. Here's a pictorial summary of what we've discovered over the last five sections.