Now assume we know the following text was enciphered using a shift:
EGDHE TGXIN XHCDI LXIWD JIBPC NUTPG HPCSS XHIPH
ITHPC SPSKT GHXIN XHCDI LXIWD JIRDB UDGIH PCSWD ETH
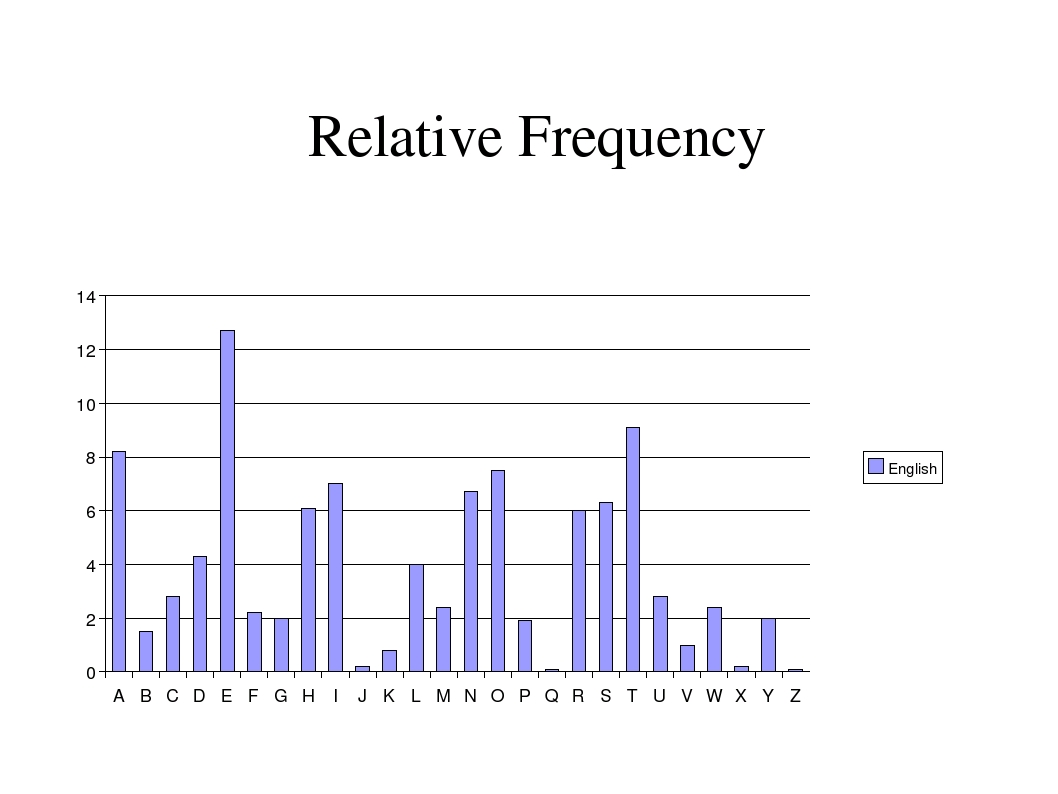
A quick letter count gives
I = 11, H =10, D = 8, P,X = 7, C=6, G,S,T = 5
E,N,W = 3, B,J,L,U=2, K,R = 1, A,F,M,O,Q,V,Y,Z=0
We can graph the cipher frequency with the English letter frequency as follows:
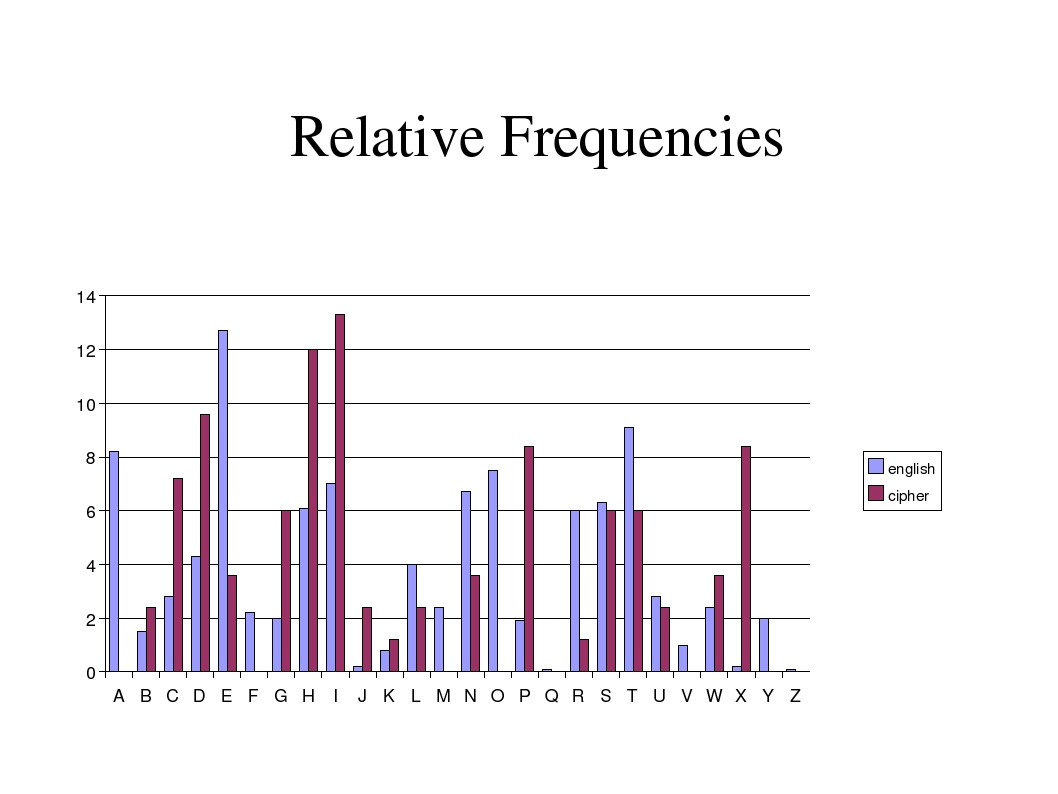
If we simply assume that E is enciphered as I we then get the following +4 shift:
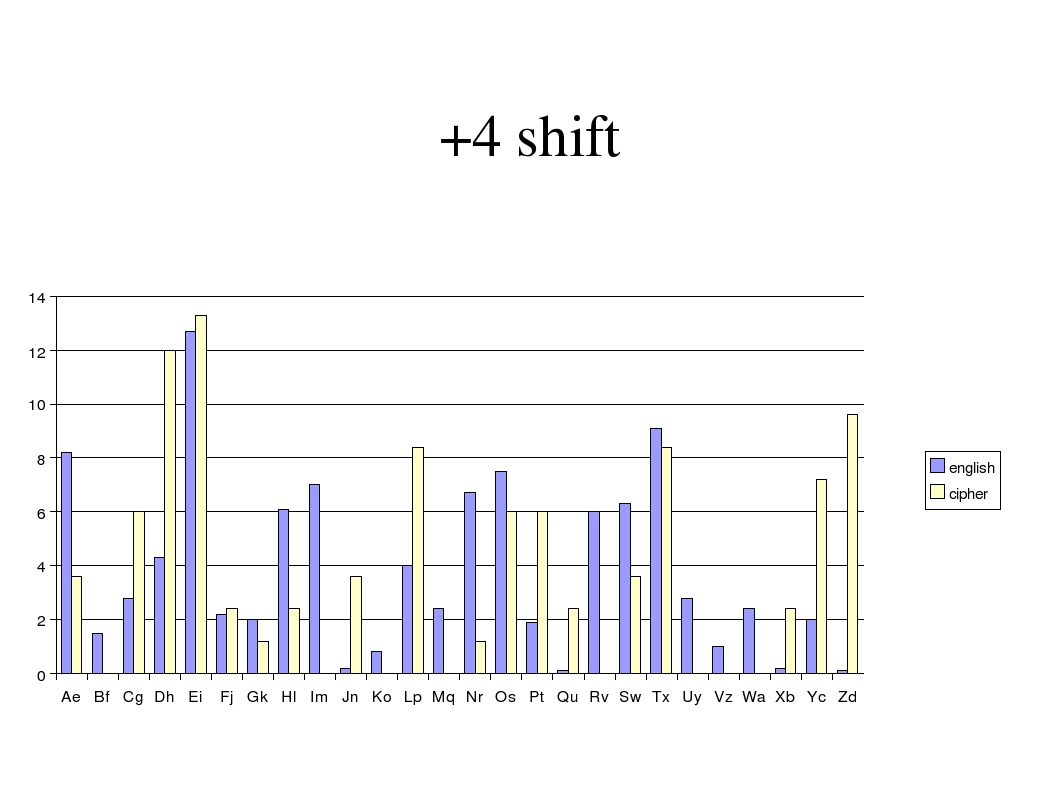
which would yield a high frequency of Y's and Z's in the plaintext. The best fit for the graphs is the following:
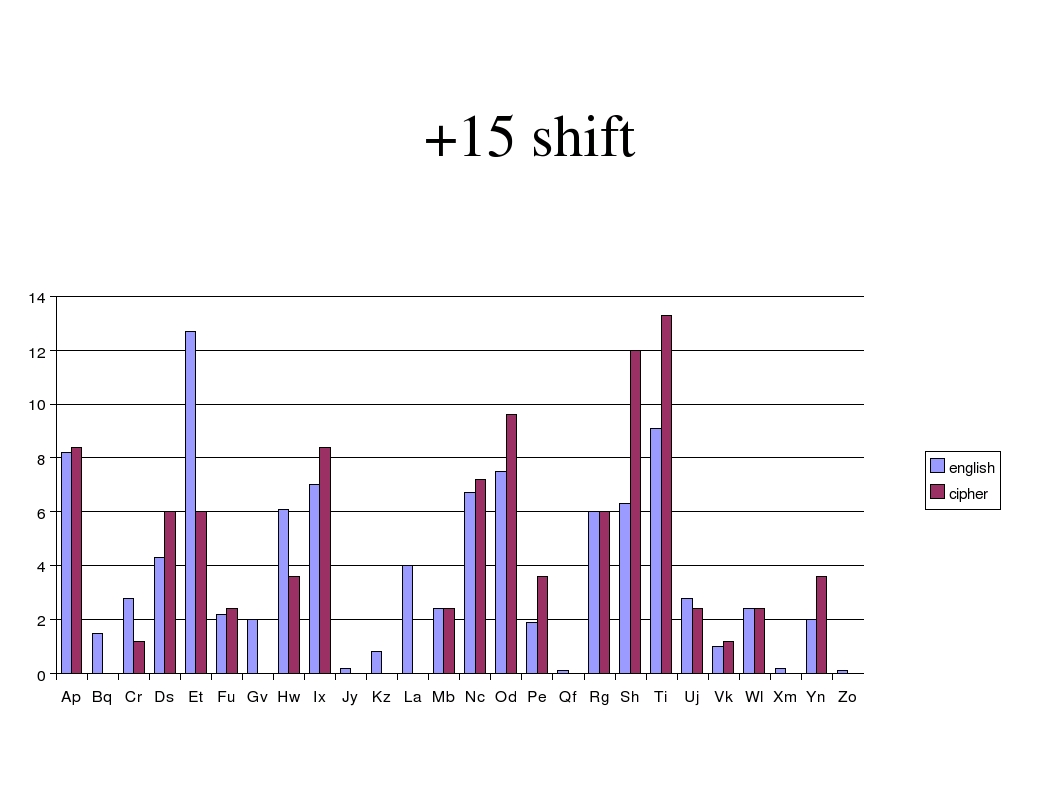
The +15 shift is given by
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O |
and has inverse a +11 shift
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K |
so that we decipher the text as:
Prosperity is not without many fears and distastes and adversity is not without comforts and hopes.