Square and Triangle

Instructions:

Download the codes for triangle and square. When the folder is the current path in matlab, the function we showcase is
e_valley(pot,p,howmany,type)
where pot is a numerical value that fixes P_{max}, p is Bernoulli parameter, howmany is the number of eigenfunctions we are solving for, type is either 'tri' for triangle or 'sq' for square.

Sample results:
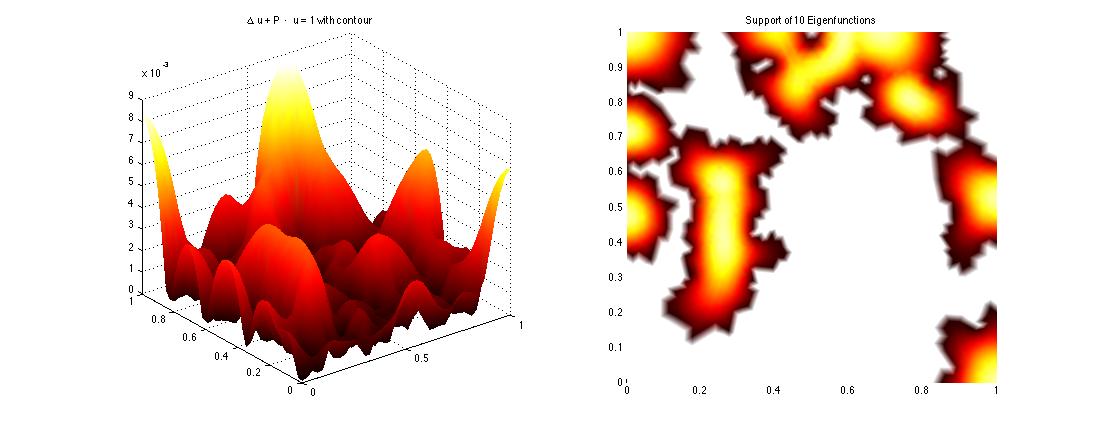
Given solutions Hu=1 and Hv = \lambda v. It is proven by Filoche and Mayboroda that |u|\ge \frac{|v|}{\lambda \|v\|_\infty} pointwise for any eigen pair v and \lambda, where \|v\|_\infty denote the supremum of |v| on the domain S.

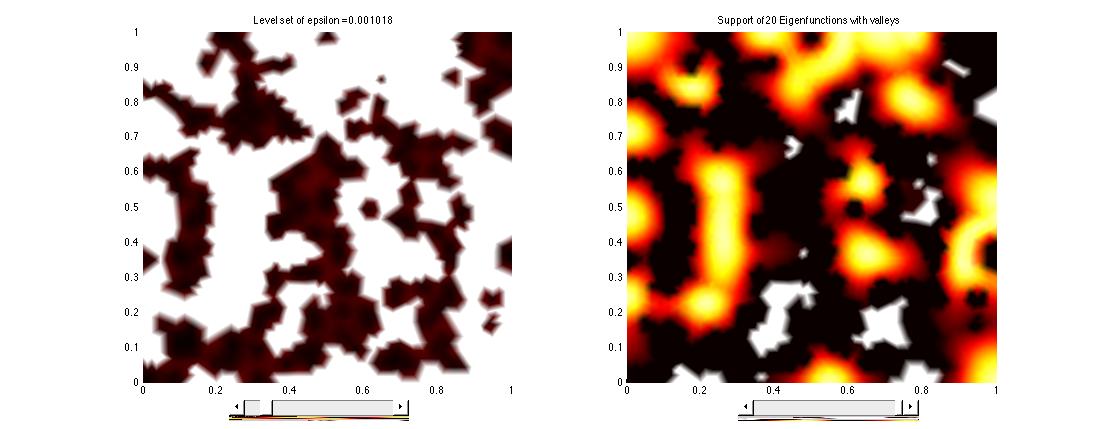
We demonstrate how u can indicate the location of the first few eigenfunctions v corresponding to the lowest eigenvalues via its cumulative level set L_\epsilon = \{x\in S. | u(x)\le \epsilon\}. We show that the supports of the first few eigenfunctions live under the highest peaks of u. L_\epsilon with adequate \epsilon serves as valleys that surround the supports of first few eigenfunctions.

Enter e_valley(10000,0.2,20,'tri'), a interactive multiplot will open. On the top row we see the solution u and the support of the first 10 eigenfunctions.
On the lower half of the plot, we could adjust the level \epsilon and the plot shows L_\epsilon. On the right hand side is an overlay of L_\epsilon with the support of the first 10 eigenfunctions.
We can adjust the number of eigenfunctions to 20.
 
Similarly if we enter e_valley(10000,0.2,20,'sq'), we will see the following
a
We can also adjust the number of eigenfunctions shown on the plots.
We will comment on the results all together in the Conclusion section on the main page.