Numb3rs Season 3 Episode 15: End of Watch

As part of this episode, Charlie launches projectiles over a distance, and determines how far they go. We will analyze the problem of how far an unpowered object goes in the presence of gravity without air resistance. We will then analyze the problem again, taking into account air resistance.

Basic Setup

We will assume that an object of mass is launched at an initial speed of at an angle of above the horizontal. The acceleration due to gravity is . We will assume that the ground underneath the projectile is essentially flat and perfectly level for the length that the projectile travels. We also will assume that the acceleration due to gravity is constant in the domain. In other words, we will ignore the curvature of the Earth.

We define the following variables:

Newton's second law states that . Here the force due to gravity is . Acceleration is the derivative of velocity over time and velocity is the derivative of position over time, so

and

Also, decomposing the initial velocity into vertical and horizontal components gives

and

Solution Without Air Resistance

Without air resistance, figuring out how far the projectile goes is easy. In this case the movement in the x-direction is effectively decoupled from the movement in the y-direction.

Vertical Motion

After launch, there is no horizontal acceleration, and the vertical acceleration is a a constant

Therefore, since the object is initially at height ,
The object is on the ground when , or when is either or . The time of is, of course, when the object launches, so the object lands at time

Horizontal Motion

How far does the projectile travel during this time? The object has an initial horizontal velocity of and travels at this speed for a time of , and so goes a total distance of

Activity 1: Optimizing Frictionless Flight

  1. How high does the projectile travel?
  2. What launch angle maximizes the height the projectile travels?
  3. What angle maximizes the horizontal distance traveled? (You may want to use the trigonometric identity )
  4. Suppose you are firing the projectile up a slope, and you want to maximize how far the projectile goes, would you aim higher or lower than your answer to the last question, or would you leave the angle the same? Why?
  5. What about firing down a slope?

Elastic Collisions

An elastic collision is a term for describing the situation when two or more bodies come close to each other interact in a way that conserves both kinetic energy and momentum. Momentum is conserved in every reaction and so is energy, but in macroscopic scale reactions, kinetic energy can be lost to heat. This is used to great effect in car bumpers, whose sole design purpose is to crush, and thereby absorb some of the kinetic energy from a collision.

At the other end of the spectrum are objects like billiard balls which have nearly perfectly elastic collisions. If one billiard ball hits another straight on, then the first billiard ball will stop moving, and the second one will travel in the same direction at nearly the same speed as the first. In reality, though, some of the kinetic energy from the first ball is converted into a small amount of heat rather than going towards propelling the second ball.

The only truly elastic collisions are extremely small, like when molecules or smaller particles hit and bounce off of each other or when black holes gravitationally interact. Even when larger astronomical bodies interact with each other gravitationally, tidal forces conspire to convert some of the kinetic energy into heat.

Solution Accounting For Air Resistance

Modeling Air Resistance

Air resistance is oftentimes modeled using a square-law, meaning that the drag force due to air is proportional to the square of the speed of the object. For a particular object, the drag force will be , where is some drag coefficient that depends on the particular shape and size of the projectile as well as on environmental factors such as air pressure. We will assume that is constant for the length of the flight.

Activity 2: Why Does Air Resistance Follow a Square-Law?

In order to determine how the force of air resistance changes as a function of the speed of an object, we need to make some reasonable assumptions concerning the underlying physics. Suppose that we model the air as a collection of individual stationary particles. An object moving through the air will collide elastically with these particles, one after another.
  1. If one individual air particle has a mass which is many orders of magnitude smaller than the mass of our flying projectile, what is the approximate speed and direction of motion of the particle after the collision?
  2. Since momentum is conserved, how much does this collision change the velocity of our projectile?
  3. If we double the speed of the projectile, how many more air particles does it collide with in the same amount of time?
  4. More generally, how does the number of collisions vary with the speed of the projectile?
  5. So, if the amount of momentum lost per collision increases linearly with speed, and the number of collisions per unit time both increase linearly with speed, then how does the total momentum lost per unit time vary with the speed of the projectile?
  6. What is the relationship between the rate of change in momentum and force applied to an object? Remember the equations , , and .
  7. Air is of course not made up of stationary particles. Particles are all moving with varying speeds whose root-mean-square is the temperature of the gas. How does the analysis of the elastic collision change when the particles are no longer sationary?
  8. What if the air particles do not automatically bounce forward? What if they are ricocheted in a random direction? Does it change your answer at all?


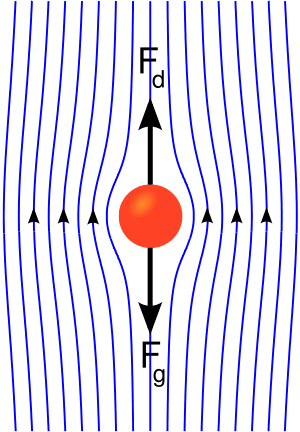
However, for projectiles with laminar flow and no turbulence, air resistance does not follow a square-law. In the derivation of the square-law, we assumed that the air particles bounce off of the projectile. When the flow is laminar (meaning smooth) as in the picture to the right, the air is only pushed around the projectile to make room for it, and then the air particles come back together largely unaffected after the projectile leaves. Here, because the air is only pushed outwards by a constant distance, irrespective of velocity, the amount of work done per unit time is proportional only to the amount of air pushed, which is proportional to the velocity of the object. So, the magnitude of the force from air resistance is proportional to speed. The direction of this force is directly opposing motion. We represent this by the equation , where is some positive constant that depends only on the shape of the object and atmospheric conditions. This is the form of air drag that we will use in the following analysis.

Decomposition into Vertical and Horizontal Components

What makes this problem tractable is again the fact that we can solve for the vertical and horizontal movements independently of each other. However, it is not obvious why this should be so. After all, in this case, we have a force whose magnitude depends on the airspeed of the object, which in turn depends on both the horizontal and the vertical components of velocity. Additionally the direction of this new force (air resistance) is not in solely the vertical or horizontal directions. The direction of the new force is always against the direction of motion. Luckily, though, we can again show that the force of air drag in the horizontal direction depends only on the horizontal velocity and the force of air drag in the vertical direction depends only on the vertical velocity by the following equations:

We will consider the horizontal and vertical motion independently.

Vertical Motion

The vertical force is a combination of gravity and air resistance :

Force is the product of acceleration and mass, and acceleration is the derivative of velocity over time :

This is a first-order linear differential equation and can be solved by the method of integrating factors to get the solution

where C is some real constant that depends on the initial velocity. Specifically, plugging in for time gives:

So the velocity, as a function of the initial conditions is :

Velocity is the derivative of position over time, so the position as a function of time is:

where C_0 is a constant that depends on the initial height of the projectile. We assume that the object is launched from the ground, so C_0 must be the constant that makes , and thus

or

Activity 3: Timing Landings with Air Resistance

  1. Is it possible to tell exactly when the projectile will hit the ground from the above equation?
  2. Is it possible to tell approximately when the projectile will hit the ground?
  3. What conditions do you need to assume?
  4. Compute the approximate time that the projectile hits the ground.

Activity 4: Vertical Motion

  1. Solve for the horizontal motion of the projectile using the same techniques as in the vertical.
  2. How far horizontally does the projectile travel before hitting the ground?
  3. How does this distance depend on the initial velocity? Is it still a square-relationship as it was when there was no air resistance?
  4. About what angle maximizes the distance traveled for a particular velocity?
  5. Can you describe qualitatively why your answer is higher or lower than the answer when there was no air resistance?
  6. How would a tail-wind or a head-wind, respectively, change the situation?
  7. What about a cross-wind?
Questions? Comments? Email me: lipa@math.cornell.edu