
In this episode, the jury returns a "not guilty" verdict on a case in which the plaintiff clearly showed that the defendant was guilty. Charlie analyzes how the jury was selected and how they reached the "non guilty" verdict, which leads him to believe that the jury was tempered with.
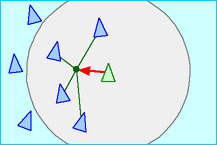
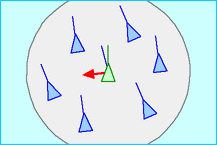
Think of a flock of geese. Each goose moves independently of others, yet it tries to stay close to the rest of the flock. The movement seems synchronized, even though each bird can only see its neighbors. What rules do you think the geese follow? Boid model analyzes this movement assuming the birds have to follow only three simple rules.
In general, Boid model simulates the movement of a group of animals, such as fish schools, herds and bird flocks. The Boid model assumes three behavior rules for the animals, which are



This model can be generalized by adding more rules and constraints, such as adding obstacles on the way, which the flock would have to avoid.
The Boids model is an example of an individual-based model, which is a simulation based on the global consequences of local interactions of members of a population. These more general models are being used in economics, ecology, biology and other sciences.
Mersenne twister is a pseudorandom number generator. This very efficient algorithm which was created in 1997, resolved many issues that the earlier algorithms had. Since this algorithm is so efficient, it has been used for jury selection. The algorithm is based on Mersenne primes, which are prime numbers that can be expressed as ''power of 2 minus one'' (i.e. primes of the form 2^n-1).
Ex: 7 and 31 are Mersenne primes since 7=2^3-1 and 31=2^5-1.
The huge open question in this subject is:
Are there infinitely many Mersenne primes? (Remember: only 47 are known!).
Let's look at one fairly simple theorem about Mersenne primes.
Theorem:
If for a positive integer n, 2^n-1 is prime, then n has to be prime.
Proof:
Note first that if r and s are positive integers, then we have
x^[rs]-1= (x^s-1) (x^[s(r-1)] + x^[s(r-2)] + ... + x^s + 1) (Check this!).
So if n is composite (say n=rs with r and s strictly between 1 and n), then
2^n-1=2^[rs]-1= (2^s-1) (2^[s(r-1)] + 2^[s(r-2)] + ... + 2^s + 1)
is also composite (because it is divisible by 2^s-1). Q.E.D.
Thus, when looking for Mersenne primes we only need to check the expressions 2^n-1 for n prime.
Reference for pictures: http://www.red3d.com/cwr/boids/