Numb3rs 106: Prime Suspect

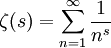
In this episode there were several mathematical topics that were mentioned. We'll discuss the Riemann hypothesis, other Millenium problems, and encryption.

Riemann Hypothesis and Millenium Problems

As was made obvious in the episode, the Riemann Hypothesis is one of the most famous conjectures in mathematics. It was originally stated in an 1859 paper written by Bernhard Riemann, and it involves the Riemann zeta-function defined as the infinite series:

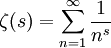
It can be shown that this series converges if the real part of s (which is a complex number in general) is greater than 1. Then it is possible to analytically continue the zeta function so that it is defined for all s with real part not equal to 1. This definition of the zeta function is analytic on its domain of definition, which is the complex analysis version of being differentiable. This basically means that with this formula we can define the function for part of the complex plane, and then we can show that there is a way of extending this to almost all of the complex plane that agrees nicely with the original definition. The Riemann Hyopthesis is that all the zeros of the continued zeta function occur either when s is a negative even integer or when the real part of s is 1/2. It is important in mathematics because it has many deep connections to prime numbers and especially to the distribution of the prime numbers (how often they occur), and there are many interesting results which have been proved to be true assuming that the Riemann hypothesis is true. For more information about various connections between other parts of math, look up the Wikipedia page about it.

As was also mentioned in the episode, the Riemann hypothesis is one of the Millennium Prize Problems. These are 7 (actually, the number recently became 6) famous mathematical problems which come with a prize of one million dollars offered by the Clay Mathematics Institute for anyone who solves them. This institute was established by Landon T. Clay and is "dedicated to increasing and disseminating mathematical knowledge." Here is a list of the problems with short descriptions:

• P versus NP: This problem deals with how hard different problems are to solve on a computer based on the length of the input for the problem. (Here the particular problem is fixed and the length of its input is allowed to vary.) A problem S is in the set P if there is a polynomial p(x) and a computer algorithm which given an input for S of length n can solve the problem in time p(n). An example is the problem of sorting a list of n numbers, which can be done in polynomial time. A problem is an NP problem if given an input and a possible solution, the solution can be checked to see if is an actual solution in polynomial time (again the polynomial is a function of the length of the input). An example of this kind of problem is the zero sum subset problem - given a set of integers is there a subset of them that sum to zero. Clearly if a problem is in P it is also in NP. The major question is whether there is a problem that is in NP but is not in P.
• The Hodge Conjecture: This conjecture is even difficult to state since it involves some very technical definitions. A (very) vague statement is that certain algebraic invariants of algebraic/geometric objects called varieties come from geometric invarients.
• The Riemann Hypothesis: This was discussed above.
• Yang-Mills existence: This is discussed in Episode 103.
• Navier-Stokes existence and smoothness: The Navier-Stokes equations describe in full detail the motion of liquids. Even though they have been known for over a century, it is still not known whether there are smooth (i.e. differentiable infinitely many times) solutions to these equations.
• The Birch and Swinnerton-Dyer conjecture: This conjecture is similar to the Hodge conjecture in that it is difficult to state, but it roughly states that there is a relationship between the number of solutions to a particular type of equation and the order of the zero of the L-function at a particular point (L-functions are related to Riemann's zeta function.)
• The Poincare conjecture: This conjecture has actually been solved in 2006 and recieved fairly wide media coverage. The two-dimensional version of the the conjecture says that if you have a surface that is simply connected (that means that if you draw a loop on the surface, you can shrink it to a point by sliding the loop continuously along the surface) and closed (it doesn't go off to infinity, and can't be stretched so that it does), then it can be deformed into a sphere. The three dimensional version of this took many years to prove.

Encryption

One of the main plot points of the episode is that the bad guys wanted the math professor to give them his solution to the Riemann hypothesis so that they could crack the encryption on major financial data. As was mentioned in the episode, many encryption algorithms depend on the fact (or apparent fact) that it is very hard to factor large numbers. One of the main encryption algorithms used today is called the RSA algorithm (the name comes from the initials of its inventors. This algorithm is also described Episode 205. As mentioned there, the main difficulty in trying to break the RSA code is that factoring numbers into prime factors can be very difficult. In particular, there is no known algorithm that factors a number n into its prime factors that is in P, i.e. runs in polynomial time as a function of log(n) (here log is used because the number of bits it takes to store a number n is log base 2 of n). It is believed that no such algorithm exists. Interestingly, there is another kind of cryptosystem that is provably difficult in the sense that if an algorithm is devised to decrypt messages in polynomial time, then this algorithm can be adapted to factor integers in polynomial time.