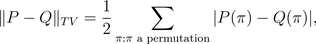Numb3rs 519: Animal Rites

A disturbed student, tied to an animal rights group, is implicated in the death of a researcher at CalSci. The arrestation attempt of this lead suspect turns into a hostage situation. In order to rescue the hostages and get into the student's mind, Charlie and Amita investigate the student's work in mathematics.  They find his math to be highly creative but formally incorrect. In some of the papers they discover an ecological version of the Prisoner's dilemma (a concept already presented in Episode 110 and Episode 321), which reveals the suspect's immense appreciation for animals.

In the beginning of the episode, while playing poker with Amita, Liz and Nikki, Larry mentions a well-known result in the mathematics of shuffling cards discovered by mathematician and magician Persi Diaconis at Stanford University. 

"Actually, Nikki makes a critical point. Persi Diaconis at Stanford proved a minimum of five shuffles are required before a deck starts to become random in the sense of variation distance described in Markov chain mixing time, but seven shuffles are optimum."

Below, we will explain this and other related results in more detail.  

Riffle shuffle

Some people lift the cards up after a riffle in order to put the two halves together. Others place the halves flat on the table with their corners touching, lifting the edges with their thumbs while pushing the two halves together.  A reason why this is one of the preferred methods of shuffling is that the cards are rarely exposed during this shuffle.

The riffle or dovetail shuffle is the most commonly used method of shuffling cards. In this shuffle the deck is cut in two halves, which are then interleaved or riffled together (see Tangent). Gilbert and Shannon in 1955 and independently Reeds in 1985 introduced a mathematical model of this type of shuffle. In this probabilistic model, the probability that exactly k cards are cut off a deck with n cards is C(n,k)/2n, where C(n,k) is the binomial coefficient; i.e. the size of the cut off has a binomial distribution with p=1/2. The k cards that have been cut are held in the left hand and the remaining n-k in the right hand. After the cut, the cards are dropped from a given hand with probability proportional to the packet size. Thus, if at some point there are c cards on the left packet and d cards have been already dropped on the table the probability that the next card is dropped from the left is c/n-d.  Diaconis in 1988 found evidence showing that this mathematical description is a reasonable approximation of the actual behavior of human shufflers.

There is a backwards description of the riffle shuffle that is helpful for its mathematical analysis. In an inverse riffle shuffle, each card in a sorted deck goes to either the left or right packet with probability 1/2. Then, the left packet is placed on top of the deck, keeping the cards in the same relative order. It turns out that the Gilbert-Shannon-Reeds model is equivalent to the inverse riffle shuffle from the probabilistic point of view. To illustrate this fact we present an example.

Suppose that we have a deck consisting of only 4 cards with initial configuration A♠ 2♠ 3♠ 4♠. Let's calculate the probability that after 1 forward riffle shuffle the new configuration is A♠ 2♠ 4♠ 3♠. In this case 3 cards are cut from the top, namely A♠ 2♠ 3♠. This happens with probability C(4,3)/24=1/4. Then the first card, 3♠, is dropped from the left packet and the second, 4♠, from the right packet.  This occurs with probability 3/4*1/3=1/4. Multiplying these two probabilities out we conclude that under the Gilbert-Shannon-Reeds model the probability of this configuration is 1/16. 

Let's now calculate the probability that after one inverse riffle shuffle we obtain the same configuration. In this case, A♠ 2♠ 4♠ go to the left packet, while 3♠ goes to the right packet. This occurs with probability 1/2*1/2*1/2*1/2=1/16. The probabilities under the two models are the same. This fact can be generalized to an arbitrary number of shuffles and the exact probability of a given configuration will be given below.

First we highlight an important observation about the riffle shuffle. Suppose that we number our cards from 1 to n. A riffle shuffle generates a permutation of this n numbers. If we denote this permutation by π, in our example above 

π(1)=1,  π(2)=2, π(3)=4 and π(4)=3, 

i.e. π(i) gives us the new position of the i-th card. A rising sequence of a permutation is a maximal consecutively increasing sequence in the permutation. For instance, in our example there are two rising sequences, namely

π(1)<π(2)<π(3) and π(4).

If we had six cards and 

π(1)=1,  π(2)=2, π(3)=4, π(4)=3, π(5)=6 and π(6)=5,

there would be three rising sequences, namely 

π(1)<π(2)<π(3), π(4)<π(5) and  π(6).

Rising sequences are the basis of a card trick called Premo by Jordan. In this trick the performer asks a spectator to riffle shuffle an unshuffled deck of cards twice, then to give it a cut and insert the top card into the pack. Give the pack a final cut and a final shuffle. The performer spreads the deck on the table and after a careful analysis selects a card. The strategy to find the correct card is explained in detail in Section 2 of Diaconis and Bayer's paper "Trailing the dovetail shuffle to its lair". The solution arises mainly from the fact that (usually) each riffle shuffle duplicates the number of rising sequences of the deck and inserting a card into the deck increases this number by one. 

It is easily seen that a permutation π of any number of cards made by a riffle shuffle has exactly two rising sequences, unless no shuffle is made whatsoever. Hence for instance the permutation of 6 cards presented above cannot come from a riffle shuffle. Conversely any permutation with 1 or 2 rising sequences can be achieved by a riffle shuffle and this type of shuffle can be characterized by this fact (see Tangent). It is not surprising then that the probability of a given configuration after an arbitrary number of riffle shuffles can be given in terms of the number of rising sequences. The following theorem was proven by Diaconis and Bayer in their celebrated paper "Trailing the dovetail shuffle to its lair" in 1992.

Theorem: If n cards are shuffled m times, then the chance that the deck is in arrangement π is

C(2m+n-r,n)/2nm, 

where r is the number of rising sequences in π.

Activity 1
    a) There are two ways to perfect riffle shuffle a deck of 2n cards. Both methods cut the deck in half perfectly. The 'out shuffle' leaves the top card in the same position while the 'in shuffle' moves it to the second position from top to bottom. These methods are also known by the name of Faro shuffle. How many in (out) Faro shuffles are needed to return a deck with 4 cards to its initial configuration? How many for a 52 cards deck? To find out more about the history of the perfect shuffle we refer the reader to Section 3 of Diaconis, Grahams and Kantor's 1983' paper titled "The mathematics of the perfect shuffle".
    b) By using Bayer and Diaconis' theorem recalculate the probabilities in the example above. Furthermore, observe that the probabilities of obtaining any configuration after one shuffle are all the same.
    c) Suppose that a deck of 8 cards has initial configuration

    A♠ 2♠ 3♠ 4♠ A♥ 2♥ 3♥ 4♥.

    Calculate the probability that after 2 riffle shuffles the new configuration is

    3♠ 3♥ 4♥ A♠ 4♠ 2♠ A♥ 2♥

Randomization

A deck of n cards is perfectly random if the probability of any of the n!=1*2...*n possible orders of the deck is the same, i.e. if the distribution of all possible orders is uniform. One possible way of measuring how random is a deck of cards after m shuffles is by measuring the total variation distance between the distribution of the permutations after the m shuffles and the distribution in a perfectly random deck. Below we explain the definition of the total variation distance in our context. We also present Persi Diaconis and Dave Bayer's famous result on the number of riffle shuffles needed to achieve a good level of randomness in a deck of cards.

The total variation distance between two probabilities P and Q over the set of permutations is defined as

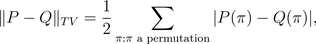
where P(π) and Q(π) denote the respective probabilities of seeing the configuration π. It can be shown that this distance is a number between 0 and 1. It can also be shown that this distance is the largest possible difference between the probabilities that the two probability distributions can assign to the same event. In the example above, all the possible 16 configurations of 4 cards after 1 riffle shuffle have the same probability equal to 1/16. There are 4!=24 possible permutations of 4 cards. Hence the total variation distance between the distribution after 1 riffle shuffle and the distribution of a perfectly random deck (for which all permutations have probability 1/24) is equal to 1/2*(1/24*8+16*(1/16-1/24))=1/3. The following table gives the total variation distance for different numbers of shuffles of decks with different number of cards.

Cards\Shuffles 1 2 3 4 5 6 7 8
25 1.000 1.000 0.999 0.775 0.437 0.231 0.114 0.056
32 1.000 1.000 1.000 0.929 0.597 0.322 0.164 0.084
52 1.000 1.000 1.000 1.000 0.924 0.614 0.334 0.167

Observe that, as Larry explained in the episode, for a regular deck with 52 cards the deck starts becoming random (i.e. the total variation distance is less than 1) after 5 shuffles and after 7 shuffles the total variation distance is less than a half. After this point, the total variation distance decreases by approximately a factor of 2 after each shuffle.  When the number of cards in the deck increases towards infinity the graph of the number of shuffle vs. the total variation distance to the uniform distribution starts looking like the graph shown in the figure below.

In a subsequent paper titled "How many shuffles to randomize a deck of cards?", L.M. Trefethen and L.N. Trefethen argued that by measuring the approximation to randomness with entropy instead of total variation distance, it takes only approximately log2n shuffles to randomize a deck of  n cards. Hence in this sense only 6 shuffles are enough to randomize a deck with 52 cards. Diaconis responded explaining that you only need four shuffles for un-suited games such as blackjack.

This phenomenon is known as the cutoff phenomenon. The number K is known as the cutoff time. Persi Diaconis and Dave Bayer proved in 1992 in a famous paper titled "Trailing the dovetail shuffle to its lair" that the cutoff time for a deck with n cards is given by (3/2)log2n, where log2n denotes the logarithm in base 2 of n (see Tangent).

Activity 2
    a) In the top in at random shuffle the top card in the deck is removed and placed back in the deck at a random position. Persi Diaconis and David Aldous proved in 1986 in a paper titled "Shuffling cards and stopping times" that the cutoff time for this shuffle is n log n, where log n denotes the natural logarithm of n. Calculate the total variation distance to perfect randomness after one top in at random shuffle of a deck with 4 cards.
    b) Calculate the total variation distance to perfect randomness after 2 riffle shuffles of a deck with 4 cards.