Phase Transition

Phase Transition Phase Transition/Critical Probability

Section 1 - Plots of probability vs max cluster size

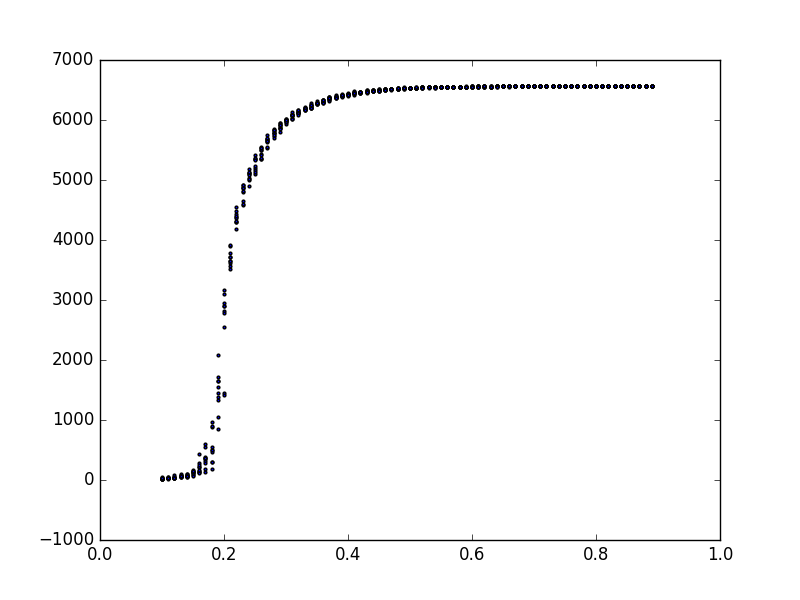
Fig. 1 - probability vs max cluster size on SG × SG

Experimental evidence suggests that the critical probability for products of Sierpinksi Gasket fractafolds is near .185

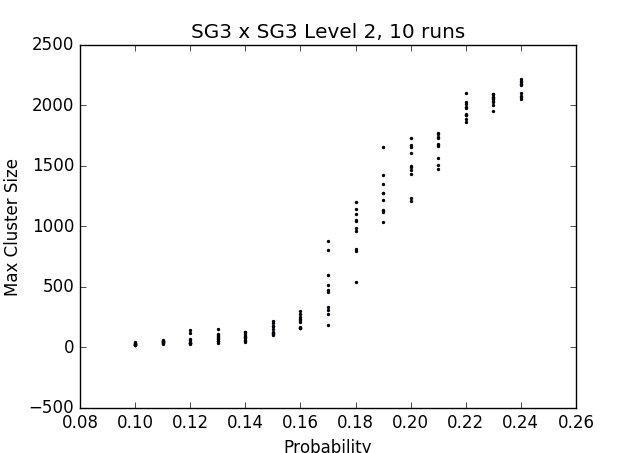
Fig. 2 - probability vs max cluster size on SG₃

Experimental evidence suggests that the critical probability for products of Sierpinksi Gasket cell graph fractafolds is near .17

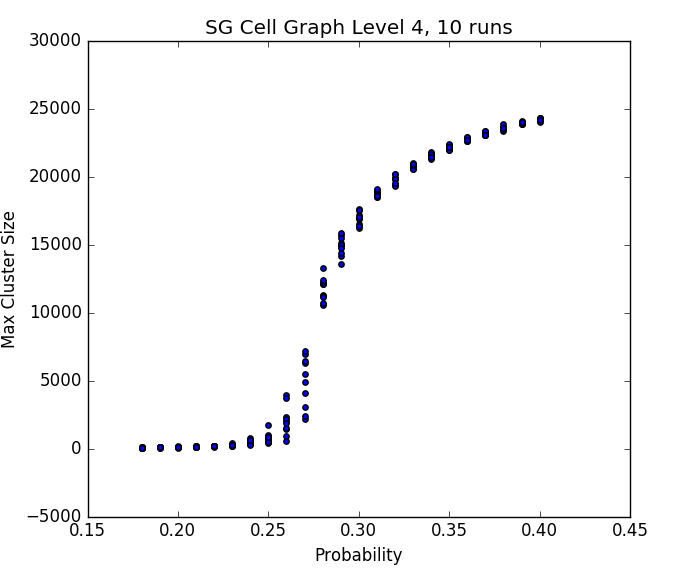
Fig. 3 - probability vs max cluster size on the cell graph version of SG X SG

Experimental evidence suggests that the critical probability for products of Sierpinksi Gasket cell graph fractafolds is near .275

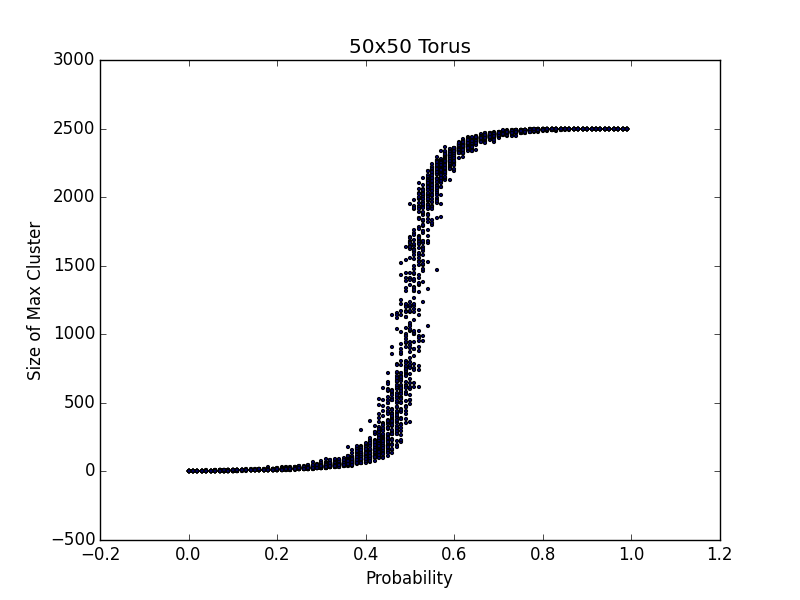
Fig. 4 - probability vs max cluster size on the torus graph

Results of our experiments fall in line with Kesten's proof that the critical probability for the infinite square lattice is .5. Note that we identify endpoints of our lattices to form a torus in order to eliminate its boundary points and force them to be 4-regular. In this way, they better represent the infinite lattice.

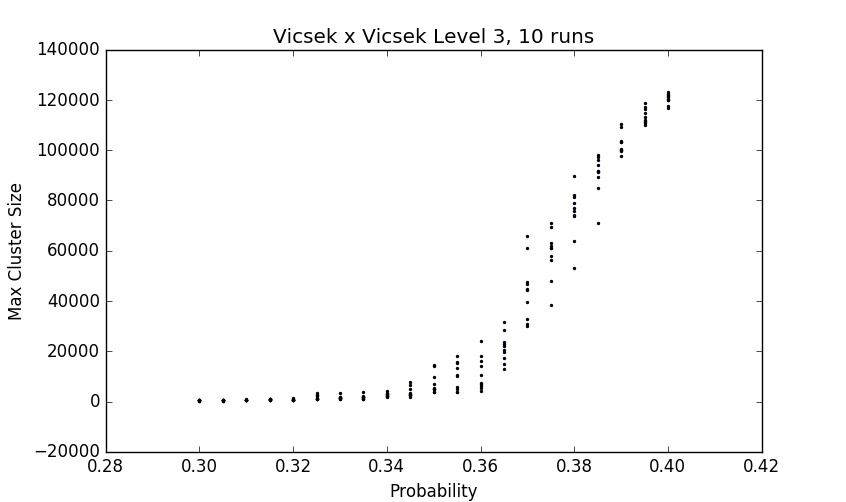
Fig. 5 - probability vs max cluster size on the Vicsek set

Experimental evidence suggests that the critical probability for these graphs is near .37

Section 2 - Locating phase transition by finding spanning clusters

Percolation theory on infinite graphs posits that in the supercritical phase we will see infinite max clusters in the parent graph. In the case of finite graphs, we could say that the analogue of an infinite cluster is one that extends from one side of the boundary of the graph to an opposite side of the boundary. We can then try to locate the phase transition by looking for the first time every run at a given probability produces a spanning max cluster. To define a spanning cluster, we use must define a boundary on the fractal product graph. To do this, take Q to be the set of boundary points in the root graph K (e.g. SG itself). Then we define the boundary of the product graph to be (K × Q) ∪ (Q × K). We then say a cluster spans its parent graph if it contains vertices on two non-intersecting sides of the boundary. Here, a side of the graph is defined to be K × {q} for some q ∈ Q.

Results on the SG × SG

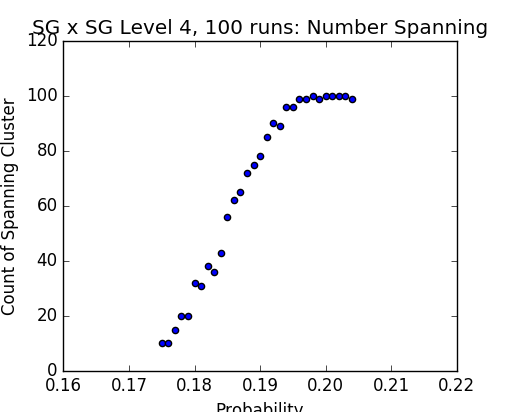
Figs. 6-8 - Probabilities vs number of spanning clusters on SG × SG

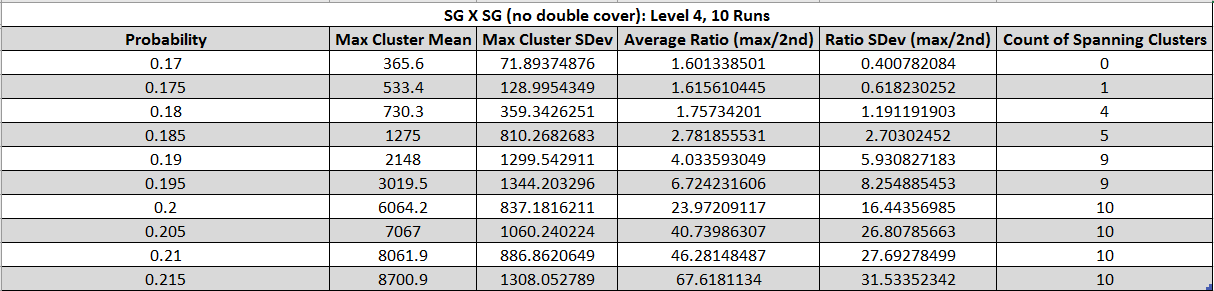
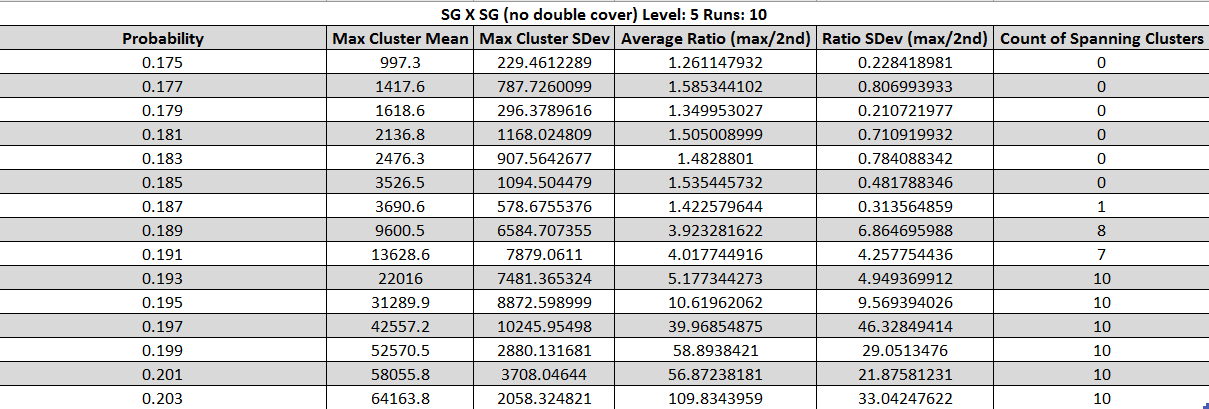Fig. 9, 10 - Tables of statistics about spanning clusters of SG × SG

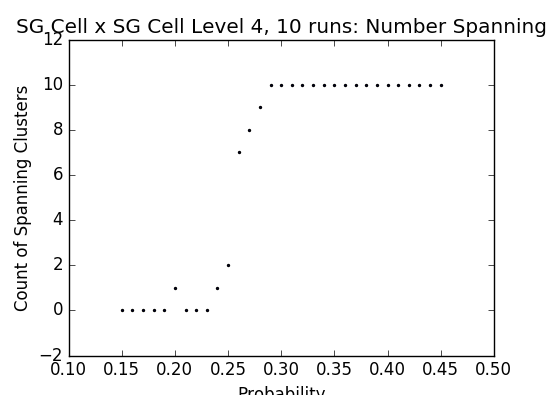
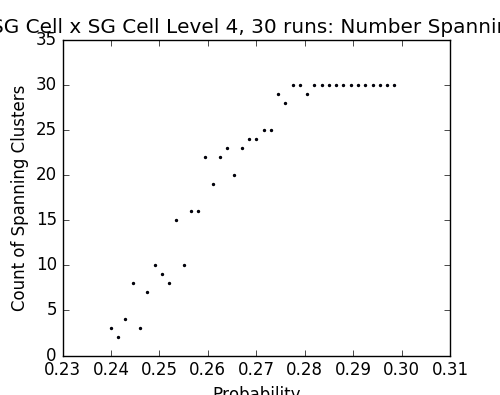
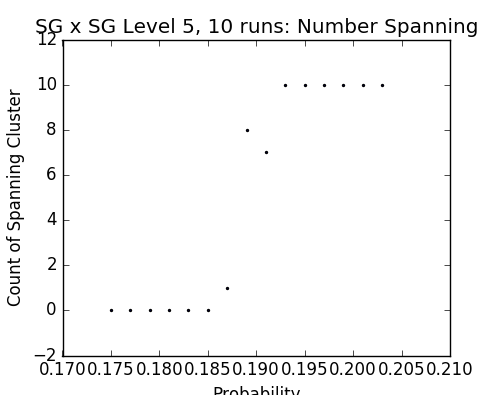
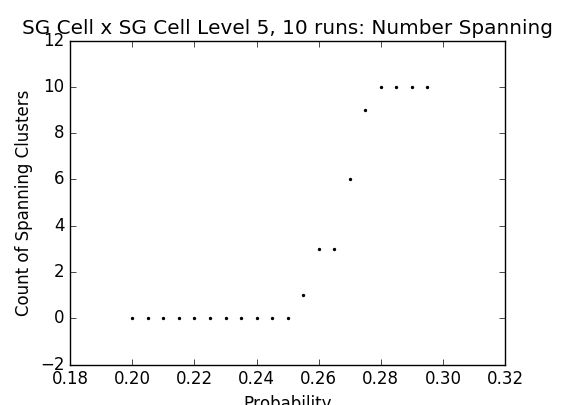Figs. 11-13 - Probabilities vs number of spanning clusters on the cell graph version of SG × SG

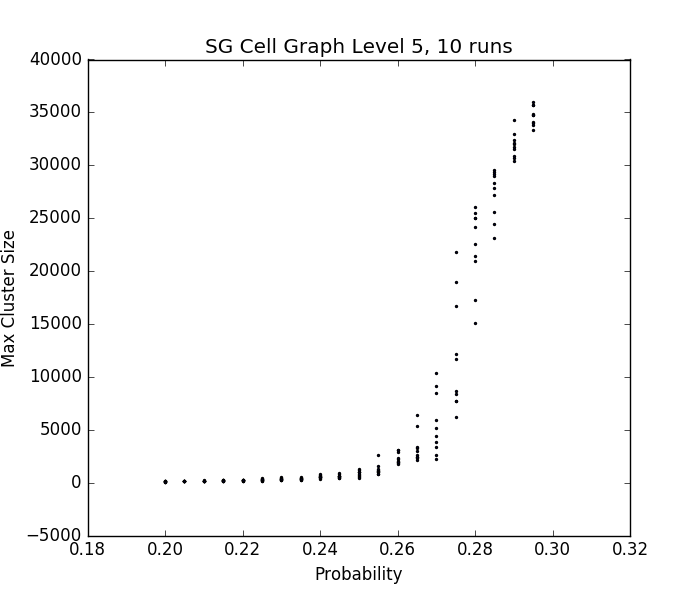
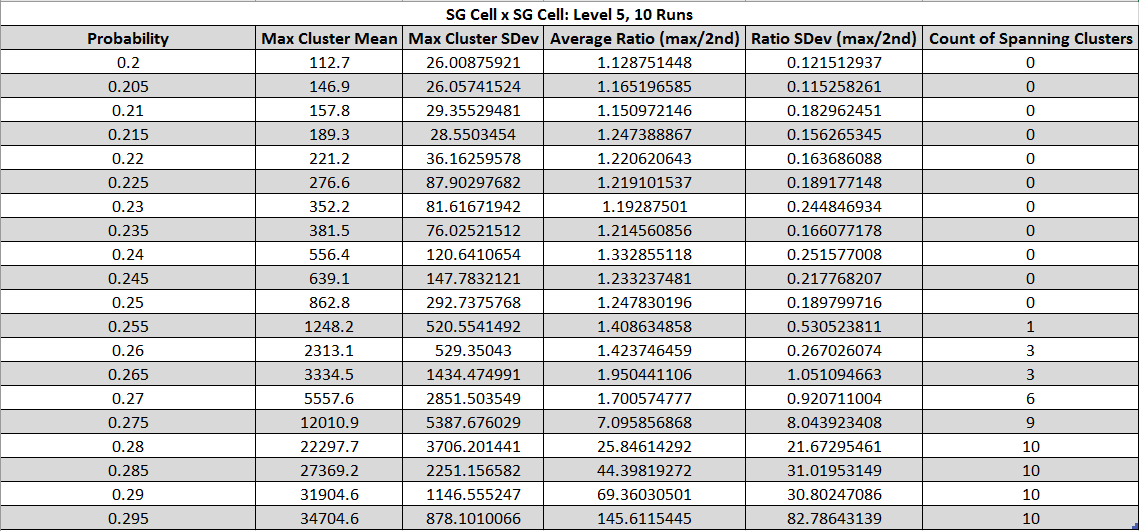Fig. 14, 15 - Plot and Table of statistics about spanning clusters of the cell graph version of SG × SG

Results on the Mistubishi gasket (SG₃)

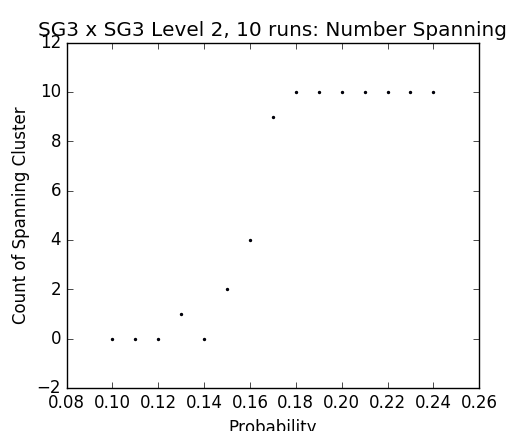Fig. 16 - p vs number of spanning clusters on SG₃

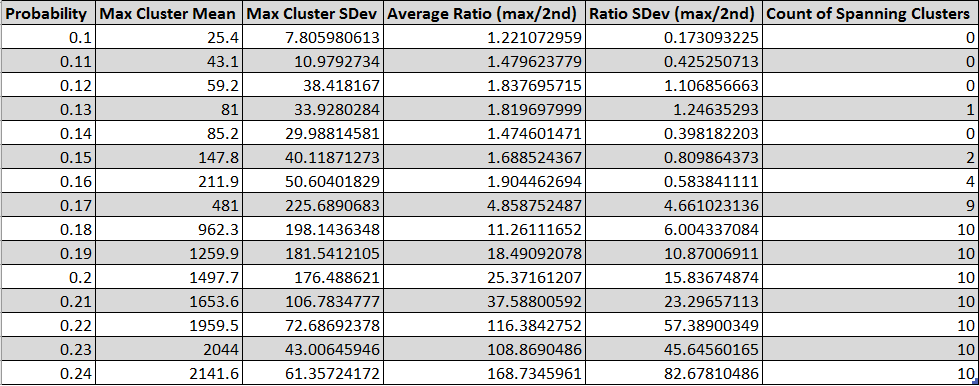Fig. 17 - Table of statistics about spanning clusters of SG₃ as p is varied Results on the lattice (no torus identifications)

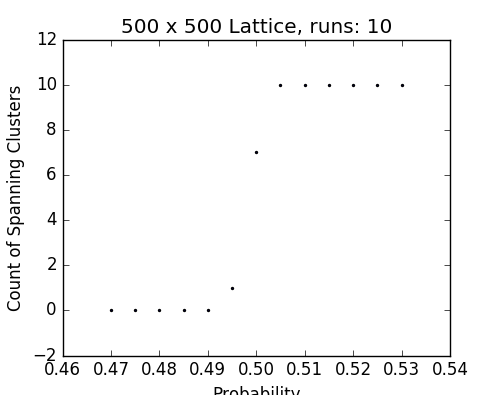Fig. 18 - p vs number of spanning clusters in a lattice

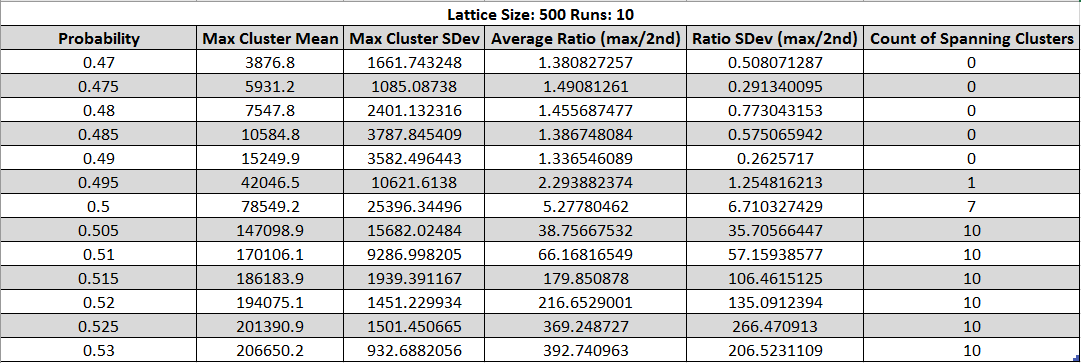Fig. 19 - Table of statistics about spanning clusters of the torus graph as p is varied Results on the the Vicsek set

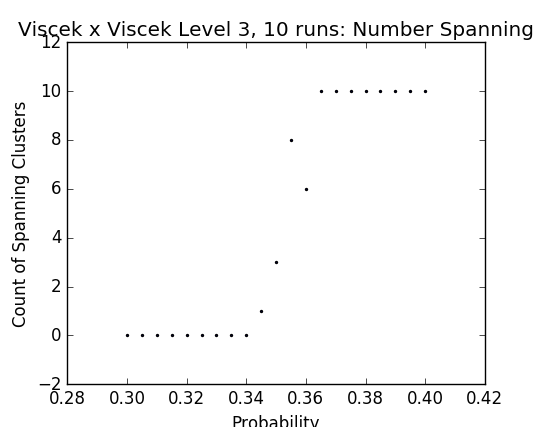Fig. 20 - p vs number of spanning clusters in a Vicsek set

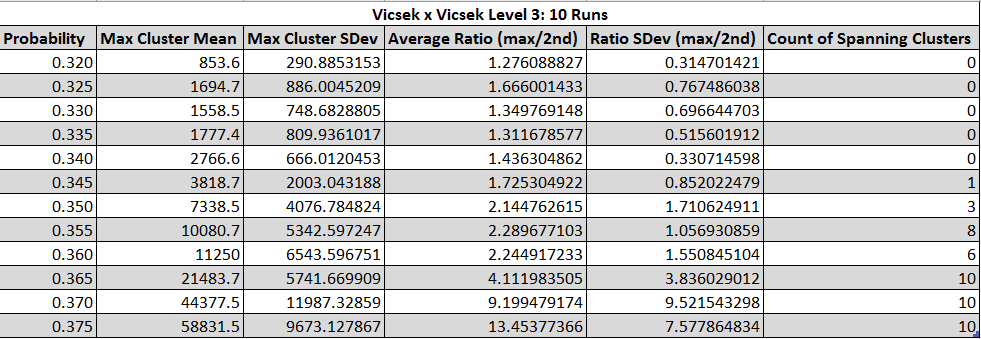Fig. 21 - Table of statistics about spanning clusters of the Vicsek set fractal as p is varied

Results on the the Magic Carpet Graph

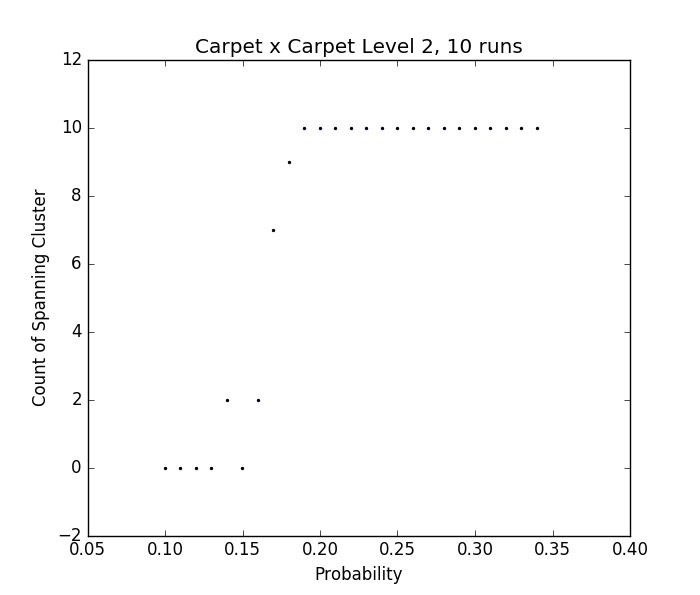Fig. 22 - p vs number of spanning clusters in the Magic Carpet

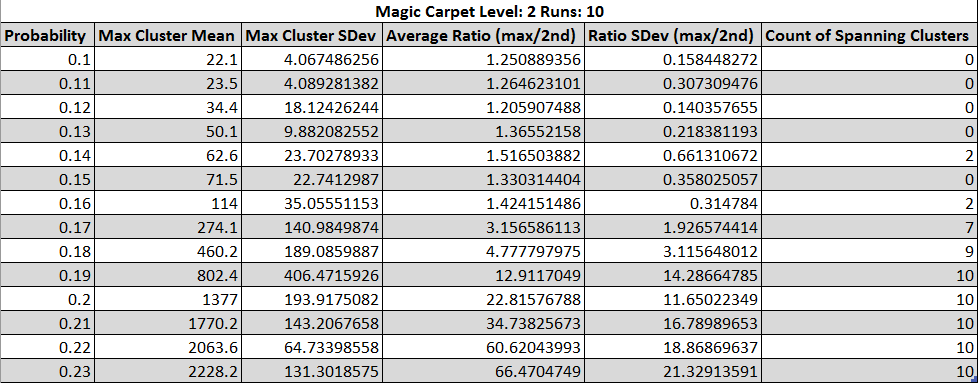Fig. 23 - Table of statistics about spanning clusters of the Magic Carpet as p is varied

Section 3 - Locating phase transition by looking at cluster size ratios
Results on SG × SG

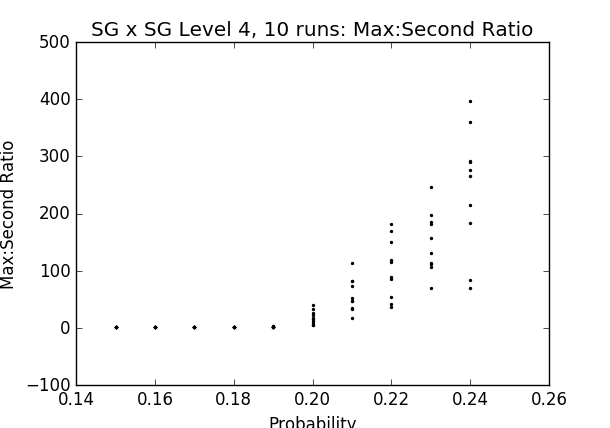Fig. 24 - p vs ratio of sizes of largest and 2nd largest clusters in percolated SG × SG graphs Results on the cell graph version of SG × SG

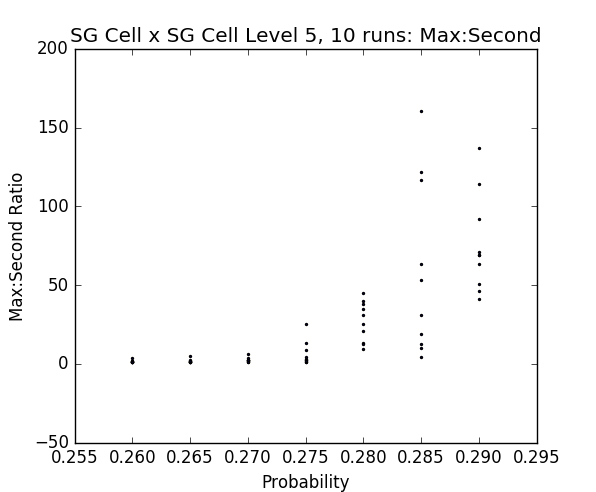Fig. 25 - p vs ratio of sizes of largest and 2nd largest clusters in percolated cell graphs Results on the the Mitsubishi gasket (SG₃)

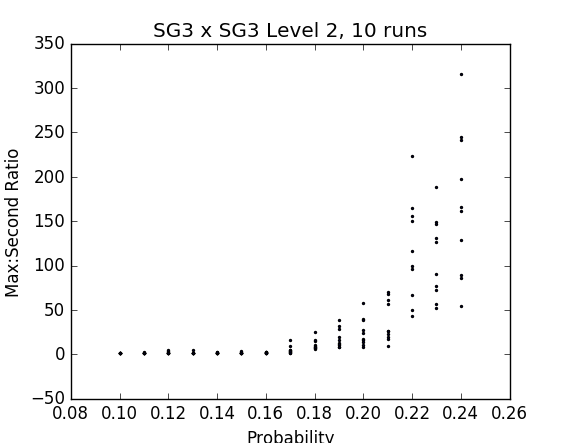Fig. 26 - p vs ratio of sizes of largest and 2nd largest clusters in percolated vicsek sets Results on the lattice

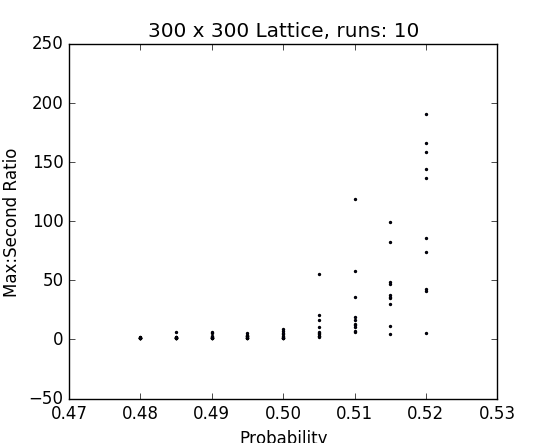
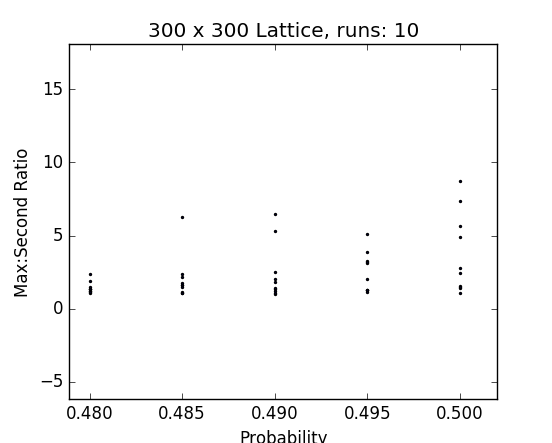Fig. 27, 28 - p vs ratio of sizes of largest and 2nd largest clusters in percolated lattice graphs Results on the Vicsek set

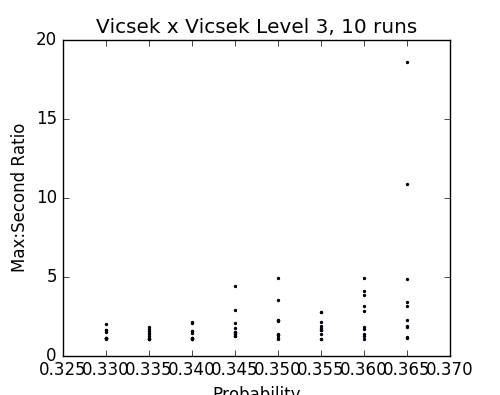
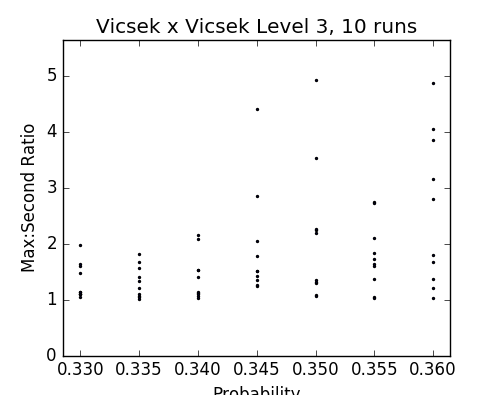Fig. 29, 30 - p vs ratio of sizes of largest and 2nd largest clusters in percolated Vicsek sets Results on the Magic Carpet

;

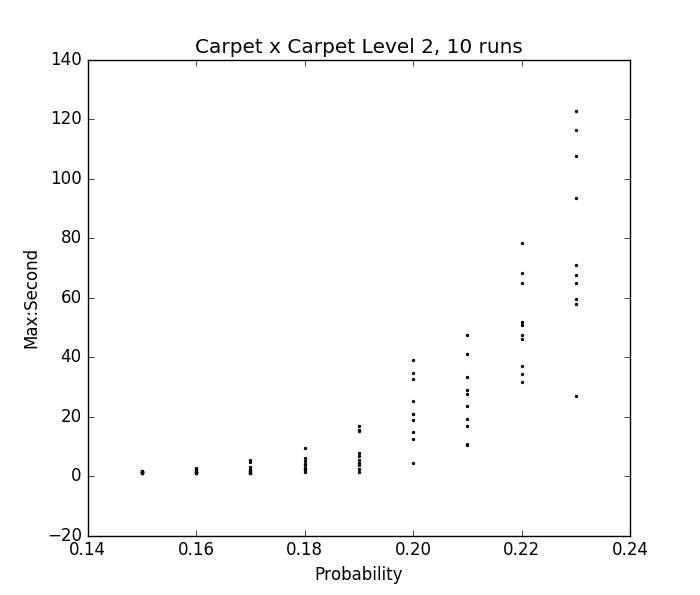
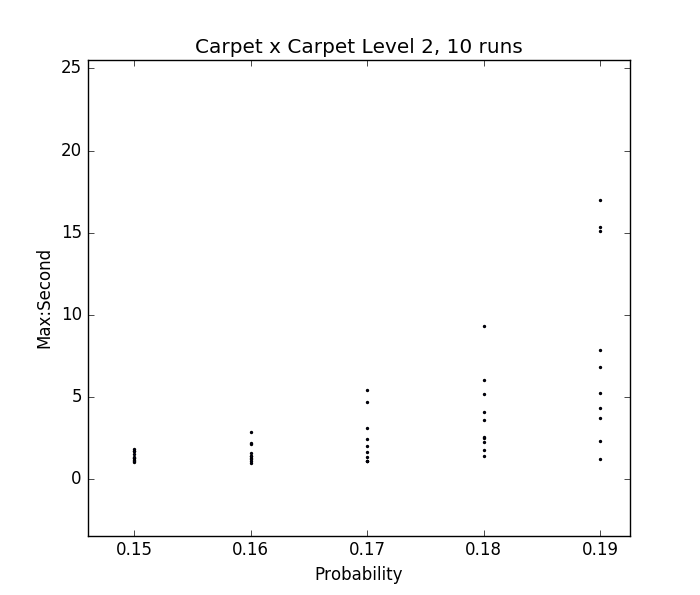Fig. 30, 31 - p vs ratio of sizes of largest and 2nd largest clusters in percolated Magic Carpet