Iancu Dima: idima1@ithaca.edu
Rachel Popp: rachel.popp@gmail.com
REU advisor: Professor Robert S. Strichartz
Research support by the National Science Foundation
through the Research Experience for Undergraduates
program at Cornell University, grant-1156350
* Any opinions, findings, and conclusions or recommendations
expressed in this material are those of the authors and do not
necessarily reflect the views of the National Science Foundation.
Introduction
A convex polyhedron is a surface that is flat (curvature = 0) everywhere except at the vertices, where it is a positive multiple of a delta mass. By the Gauss-Bonnet theorem, the sum of curvature over the vertices equals 4π. We began this REU with an interest in building a surface which is a limit of convex polyhedra so that the curvature is distributed according to a fractal measure of a total mass 4π. We refer to the surface we explored as the SG-octahedron and it is constructed by taking a regular octahedron and putting a standard SG measure on half the faces with total mass π. This measure is a limit of discrete measures with weights at the 2.(3m+1) vertices at each of the 4 SGs, giving each vertex a weight of 2π/3m+1. We enforce the flat faces (faces with 0-curvature) to be equilateral triangles (this includes half of the faces on the original octahedron, and the interior triangles on the SG-faces). At each level m of discrete approximation the curvature determines the angles which determine the side lengths up to a constant. The images above show discrete approximations at levels m=1 in blue and m=2 in green of the SG-octahedron, with curvature distributed across the colored SG-faces and folding occuring on the golden flat-faces. We used the information in the next sections to build a Matlab code which implements the finite element method over different levels m of the SG-octahedron and further subdivision at each level. We attatch the final code for the FEM as well as plots of normalized eigenvalues, which will be used to approximate the spectrum of the laplacian of the SG-octahedron.
Coordinate System
We can denote angle positions on a curved face uniquely by utelizing the usual SG notation. Let w be the word that names the triangle and i={0,1,2} be the top, bottom left, and bottom right vertices of any such triangle, respectively. Then we denote a(w,i) the angle value in the ith vertex of triangle w. Because of the symmetry of SG-octahedron, we are interested in only the top 1/3 of the curved faces as shown in the figures below.

Angles
We can represent angles by their a-values where the angle = π/3 + a(π/3m+1). By curvature, trigonometry, and symmetry, we uniquely fill in the angles of triangles on curved faces by the following rules:
1. a(w, 0) + a(w, 1) + a(w, 2) = 0
2. a(w'i, j) + a(w'j, i) = -2 (i≠j)
3. a(0...0, 0) = 3m - 1
4. a(w, j) unchanged by systematic in-
terchange 1 <—> 2
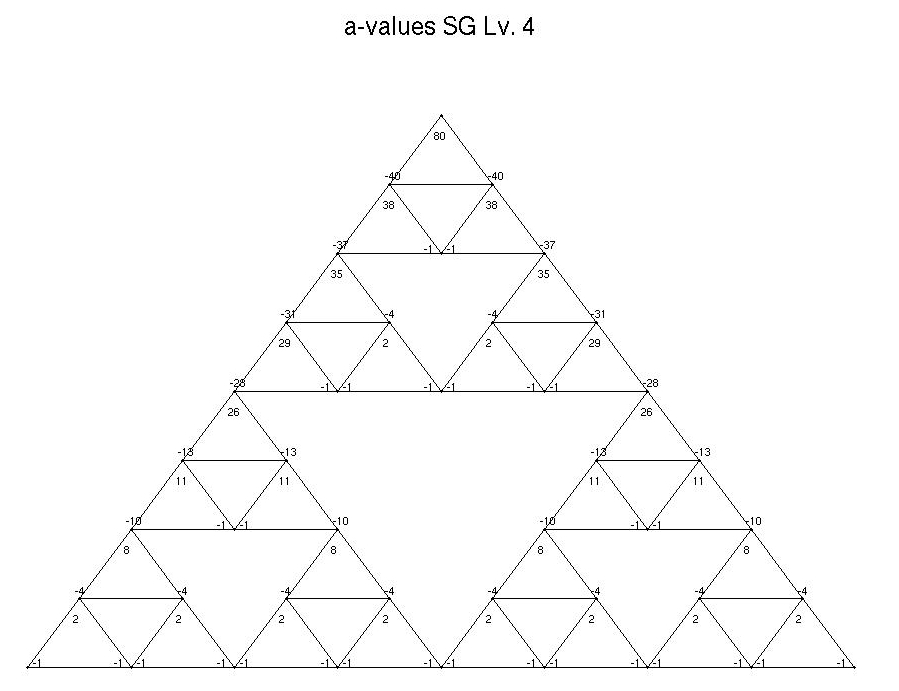
Replacing a with b=a-1 we found the following formula for the positive b-values on the outer edge of the top 1/3 of the curved face. This formula takes the binary coordinates from our coordinate system as inputs and gives b-values as outputs:

From here, we can tell Matlab to match each coordinate with its appropriate a-value by mapping into the SG face to different degrees, then counting in binary along diagonals with the remaining digits.
The following matlab code plots the diagrams above. Run them by downloading the folder MATLAB and typing PlotCoords(m), PlotA(m), or PlotAngles(m) into the command window for the desired level m.
Lengths
We associate an unknown length with the known angle opposite of it in each triangle. We know the position of these from our coordinate system and have used this to build a Matlab function to solve for lengths. This function takes as input the level m and a length constant k and uses law of sines and length relations to build a system of equations which then uniquely solves for lengths. By "length relations" we mean the relations enforced on the lengths given symmetry and that the interior triangles and non-SG faces are equilateral.
FEM
To implement the finite element method, we need a Gram matrix and an energy matrix which are sparse matrices filled with contributions from areas of triangles for each of the vertices. In the Matlab function "facegluer" we utilize the coordinate system to give each vertex a unique name from the natural numbers. Although there are no vertices and therefore zero curvature on the non-SG face, the vertices added to the SG-faces cause the non-SG faces to fold as shown in gold in the figure below. This creates trapazoids which must be triangulated for the FEM. We do this by adding vertices to the top of each trapazoid and edges connecting this vertex to the bottom two vertices of the trapazoid. At levels higher than m=2, folding occurs in the interior triangles of the SG faces as well.
Resulting Eigenvalues