17. CONICS
These problems are inspired by David Dennis, who
wrote a Phd thesis at Cornell making use of the Sketchpad. Consider the curves formed by the following methods:
·
Sections
of a cone cut by a plane. (Note: a
cone is an infinite surface, with upper and lower parts meeting at a vertex.)
·
Family
of graphs of quadratic polynomials ax2
+ bxy + cy2 + dx + ey +f = 0
·
The
path of a ball thrown from a bridge. Or
the graph of distance vs. time for a falling object, diver, parachute jumper,
etc.
·
Various
loci formed from curve drawing devices such as string and two nails.
QUESTIONS:
How
do we know that a plane curve we draw or construct as a locus a
"conic"?
How
do we know that the x-y equations of these curves are quadratics?
How
do we know that curves drawn by some methods are equivalent to any of the other
definitions?
(Following
this page is a list of 12 methods, among many, for drawing conics.)
More
specifically: How can you translate the
parameters of one of these curves to another?
That is, if you know the length of the ladder and
position of the cup in A. how do you find the equivalent length of string and
position of pins to draw the identical curve in B?
·
A
ladder stands against a building. The
bottom begins to slide away from the building and the top comes down the side
of the building. A cup is sitting on
one rung of the ladder. What path does
the cup trace out as the ladder falls down?
·
String
and points: given two pins and a string loop of given length around the pins,
you can draw a curve by keeping the pencil against the string.
What kind of curve do you get? For a given length string and points, what size ladder and where is the cat to get the same curve?
CONIC:
Curve drawing, algebraic, and other geometric definitions.
Make sketches for several of
these methods on the Sketchpad. As
asked above, think about how to translate one set of parameter definitions into
any other. Which are most primary?
a. STRING AND NAILS TRICK:
Given two points A and B, and
a constant d: draw the locus of all
points P in a plane such that the sum of the distances AP and BP is a constant
d.
PARAMETERS:
distance AB and distance d.
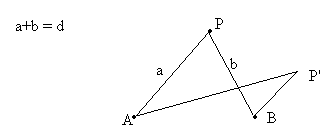
NOTE: There is a similar method for hyperbolas.
b. CROSSED
PARALLELOGRAM
Start with a crossed
parallelogram ABCD (a parallelogram in which you cross the two longer sides)
with side AB fixed. Move point C around
(it lies on a circle with center B) and trace the intersection point P of BC
and AD. Show that this construction is
the same as the locus in #1.
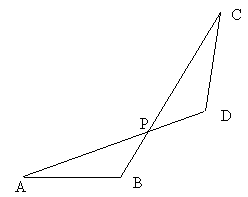
VARIATION: suppose you start with a crossed
quadrilateral, not a parallelogram, with fixed side lengths. What curve do you get?
c. CARPENTER SQUARE/LADDER FALL
Given two perpendicular axes,
a segment AB of constant length moves so that one endpoint is on each axis.
Point P on the segment AB traces a locus on the plane.
PARAMETERS:
length AB and AP.
PROBLEM:
show that this construction gives the same locus as problem 1. a.
given a total length and distance for points in #1, tell what the
corresponding ladder length and position is for the point on the ladder that
will draw an identical curve.
b. Given ladder length and position of point,
find corresponding total distance and distance apart for points in method #1.
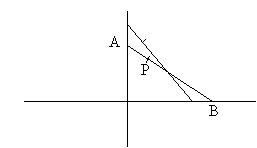
VARIATION:
try axes which are not at right angles.
Let the ends of the segment AB move on some other kinds of curves.
points
d. BENT STRAW
Segment AB is hinged at the
midpoint D. Point A stays fixed while
point B moves on a line. Point P on
segment BD traces a locus in a plane.
PARAMETERS:
lengths AD and BP.
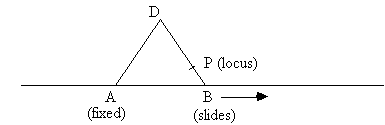
VARIATION::
try AD not equal to BD
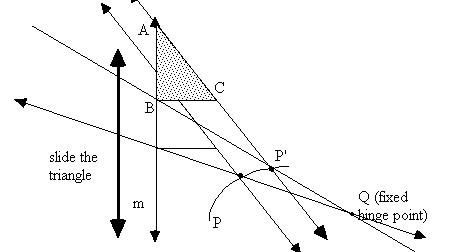
e. Da VINCI
Triangle ABC slides up and
down with side AB along line m. Q is a
fixed point not on the line m. The
intersection point P of lines QB and AC traces a curve as the triangle slides
up and down. (line QB pivots on Q, AC
stays parallel to itself.)
f. PAPER FOLDING:
Start with a piece of waxed
paper, a line l and a point A not on l.
Fold the paper so point A lands on l, and crease. Keep doing this for several positions of A
landing on l. You get the envelope of a
curve.
NOTE:
try this also with a circle, and a point A inside, or outside, or on the
circle. What kind of curve do you get
in each case?
g. RATIO constructions of curves.
- Given Three segments a,b,c, show how to construct
a fourth segment d so that:
a/b = c/d
- If b and c are each 1 unit, we get a/1 = 1/d, or a = 1/d.
Show how to use the
proportion construction to draw the locus of the point (x,y) so that y = 1/x.
Show how to draw the
locus y = c/x by letting b=1 and c be
a "parameter" (variable length segment) to show the family of
curves.
- Show how to write y = x2 as a suitable proportion with four terms,
so that we can draw the locus of y in terms of changing x. You need to have a unit 1 of course.
It would be nice to modify
your construction in a. to use rectangles instead of triangles, so you can
start with a square with side x, vertex at the origin, and hav the segment y be
constructed in the y-direction so as x changes you trace out the parabola (x,
x2).
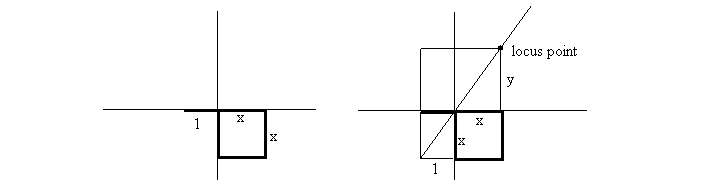
- Henderson
parabola/hyperbola.
We can draw points for dy = x2,
where d is a parameter segment.
Start with a square with side
x and unit segment u on negative x axis.
Construct the rest of the rectangluar figure on the right by making the
lower left rectangle (1x) similar to the upper right (xy). Since 1/x=x/y, we have y=x2. Let x vary to get the curve.
PARAMETER:
length of the unit.
NOTE:
show how to modify this construct to get the hyperbola y = 1/x.
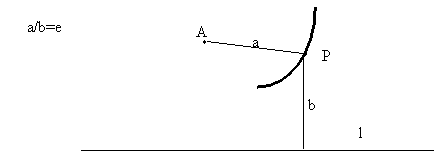
h.ECCENTRICITY
Start with a line l and a
point A not on l. Draw the curve which
is the locus of points P such that PA = Pl
(distance P to line l).

GENERALIZED
ECCENTRICITY: Given any number e, the
eccentricity, construct the locus of all points Q such that the ratio of the
distance from P to A to the distance from P to line l is e. e<1 is an ellipse, e>1 a hyperbola.
PARAMETERS:
distance from P to l, and eccentricity e.
i. PASCAL'S THEOREM family of conics:
Theorem: Given any 6 points
a1 a2 a3, b1 b2 b3 on a conic. Then the
intersections of the three pairs of lines a1b2,a2b1 a1b3,a3b1 and a2b3,a3b2 are collinear.
Corollary: 5 non-collinear
points determine a conic.
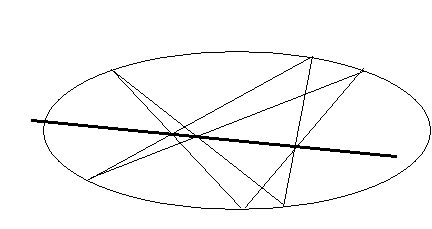
ACTION: Given any 5 non-collinear points, you can
find the locus of a 6th point as it traces the conic by working backwards in
the theorem.
(HARD) QUESTION: what
positions of the 5 points will give what conics?
j. A conic is a section of a cone cut by a
plane.
How
do we know any of the curves on this page are equivalent to this definition?
k. Family of
graphs of quadratic polynomials ax2
+ bxy + cy2 + dx + ey +f = 0
l. Ellipse/Hyperbola
Investigation
Follow the instructions carefully and consult your neighbors or your teacher if you are unsure of what to do at any step. Jot down notes, either in complete sentences or fragments, each time you are asked to make observations.
1. Open a new sketch.
2. Construct a circle, a point on the circle and a point in its interior.
3. Name each of the points appropriately. (You may want to agree as a class what to name certain objects so that you may talk about them as you move through the investigation.)
4. Draw a line segment through the interior point and the point on the circle. Construct its midpoint. Construct a line perpendicular to this line through the midpoint.
5. Construct a line through the center of the circle and the point on the circle.
6. Construct a point at the intersection of the line along the radius and the constructed line. Call this point the locus maker.
7. Select "locus maker". Go to the Display Menu and select Trace point. This command will now trace the point locus maker as you move objects on the sketch.
8. Move the point on the circle around the circle slowly in one direction. What kind of object is being created by the trace? Write a statement describing the locus of points.
9. We can get the program to move the point around the circle by creating an animation button. Select the point on the circle and the circle itself. Go to the Edit Menu and select Animation under Action Button.1 An animation button will appear. Double click on the button and observe what happens. Make a statement.
10. We can get a permanent locus of points by selecting the point on the circle and the locus maker together. Go to the Construct Menu and select locus.
11. Hide whatever you think is appropriate based upon what you think intrudes in the sketch. You should display at least the circle, the point on the circle, the locus maker, the center of the circle, the interior point and the point that controls the radius of the circle. Keep the locus on, but remove the trace command.
12. Construct segments connecting the center and the locus maker and the interior point and the locus maker.
13. Calculate the lengths of each of the new segments and the sum of the two lengths. Click the animation button and observe what happens. (Wow!) Describe what is happening in a sentence or two.
14. Now move the interior point outside the circle and click the animation button. (You may want to rename the point "exterior point" now.) Describe what is happening in a sentence or two. In particular, observe the sum of the lengths you created. What do you notice?
15. Finally, find the difference between the two lengths. Click the animation button and observe. Describe what is happening.
16. Answer any or all of the following questions by manipulating the sketch you have created. (Perhaps you should save now if you want to keep this sketch.)
- What happens when you change the radius of the circle; observe all measurements.
- What is the relationship between the sum and the difference when you move the point inside and outside the circle?
- What happens when the interior/exterior point lies on the circle?
- What
other phenomena do you observe? Jot
them down. Share with your neighbors.