5. CLASSIFYING QUADRILATERALS

The usual classification of quadrilaterals involves equal sides and parallel lines.

a. Try constructing a quadrilateral ABCD which stays a

parallelogram, rectangle, square

in the most general way you can. Notice that not all the vertices move the figure in the same way. Try constructing each by several methods, and notice the different movements.

b. You can also classify quadrilaterals by the kinds and number of symmetries they have. This works real well on Sketchpad. Try the following.

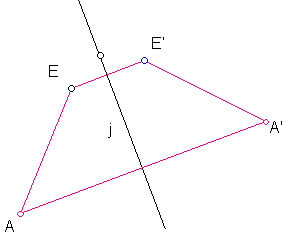
i. Construct quadrilateral ABCD with one line of reflection symmetry through a side.

DRAW a line j. Mark it as a mirror.

Draw any segment EA.

REFLECT EA across j: include endpoints.

Draw EE' and AA'

Move the vertices and see what happens. Move E or A across j. etc.

What kinds of figures can you get?

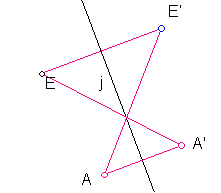
ii. Two lines of mirror symmetry through sides:

DRAW a line j. Mark it as a mirror.

Draw any point E. REFLECT across j to E’: Draw E E'

Draw another line n. Mark n a mirror.

Reflect E across n to E"

Draw EE"

Reflect E' across n to G

Select j and mark mirror j.

Reflect E" across j to H.

You should have this picture:

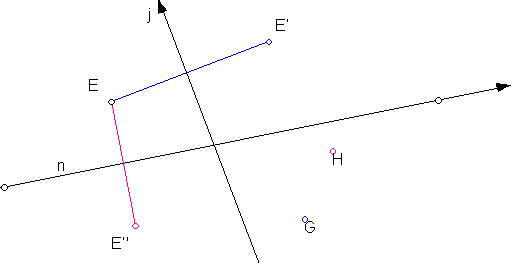
Draw in segments E'G and E"H to see the two possible quadrilaterals.

Move the position of n so that G coincides with H.

What do you observe? WHAT KIND OF FIGURES CAN YOU GET?

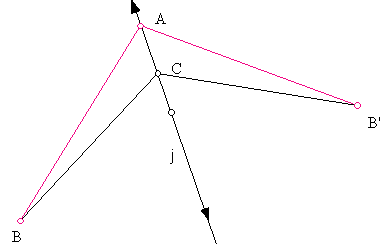
iii. One line of symmetry through vertex:

Draw line j. Mark it a mirror.

Construct a point A and C on j.

Draw any point B. Refelect B to B'

Complete the quadrilateral ABCB'

Move the mirror. Move A. Move B (on both sides of j.)

WHAT KIND OF FIGURES CAN YOU GET?

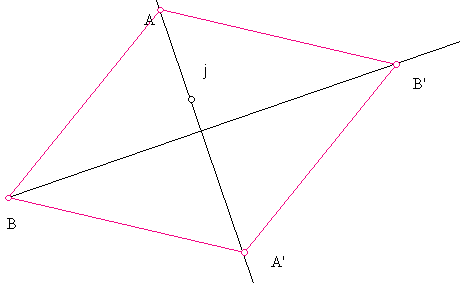
iv. Two lines of symmetry through vertices.

Draw line j. Mark it a mirror.

Construct a point A on j.

Draw any point B. Refelect B to B'

Draw line BB'

Mark BB' a mirror

Reflect A over BB' to A'

Complete the quadrilateral ABB'A'.

Move the mirror, move A, move B or B' and A'.

What properties does ABB'A' have?

WHAT KINDS OF FIGURE CAN YOU GET?

v. CONSTRUCT A QUAD WITH CENTRAL (HALF-TURN) SYMMETRY ABOUT A GIVEN POINT P.

WHAT KIND OF FIGURE CAN YOU GET?

HERE ARE SOME OF THE QUADRILATERALS BY SYMMETRY