CALCULUS INSPIRED MAX-MIN GEOMETRIC PROBLEMS

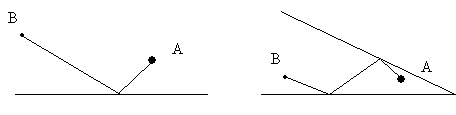
10. RIVER PROBLEM:

a. You start at a town A and have to get water from stream l. Show the shortest path.

b. Suppose you have to get water from TWO streams, l and m. What is the shortest path?

.

11. ANGLE/KICKER INVESTIGATIONS

a. Given a segment AB. Find the locus of all points C such that <ACB is 30 degrees.

Given m, find locus of points C such that <ACB has measure m.

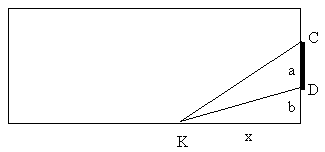
b. A soccer field has goal width a situated symmetrically on the end, distance b from corner of the field to D, the end of the goal. For given a and b, what is the best position for a kicker K on the sidelines? (neglecting the effect of distance from the goal). In other words: where will K have the largest kicking angle?

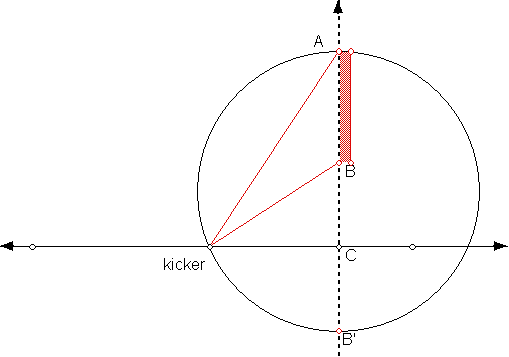
KICKER DISCUSSION:

The best position for the kicker happens where triangles ACK and KCB are similar: i.e. <AKC = <KBC.

Another way to say this is that KC is the geometric mean of CB and CA.

A nice way to find K is to extend AC to B' so BC = B'C.

Make segment AB' and draw a circle with diameter AA'.

Where the circle intersects the "sideline" is the best kick position.

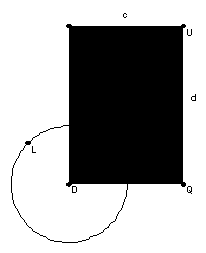
12. DOUG’s paper fold

This problem came by way of Doug Ahlfors. It was a calculus problem, but he wanted to see how to sketch it: and more importantly, WHY the solution came out as it did. We found that the experience of this movement in terms of the geometry is much more insightful than the formalism of the calculus solution--and even suggests how to tackle the calculus.

PROBLEM: Fold corner A of a rectangular paper ABCD to point P on side CD. Let this corner point P slide along C to get different folds EF.

a. How do you construct this on sketchpad? (the attempt to do so will lead you to understanding the geometry of the situation in terms of the position of P.)

b. For which position of P is the area Maximum? Minimum?

c. What is the max/min of the length of the fold?

d. EXTENSION: What if the quadrilateral ABCD is not a rectangle?

13. Doug's minimum perimeter problem for a triangle.

14. Roe rectangle.

Construct all rectangles so that the distances of each of the four vertices DTUQ to point M stay fixed. For which rectangle is the area maximum? Minimum?

This is a great problem for which the minimum solution is NOT a square. The problem is from an article by Roe, that I have lost some time ago. Tracing the locus of point U with respect to M gives a family of courves. And perhaps gives some clue as to the reason for the solution.

15. STEINER POINTS

A very practical problem for building railway stations: Given 3 (or more) points ABC, find the point P such that the sum of the distances to A, B and C is minimal.

You can do this one by trial and error, or try to think about the position of P.

Here is what happens when you draw the locus of points P for which the distance is minimal, for C moving on a line.