Math 3340: Abstract Algebra

Prof. Allen Knutson

Final exam, with answers

Grades: 70+ = A, 50-70 = B, 30-50 = C, 10-30 = D. Score distribution:

TTh 10:10-11:25, Baker 335

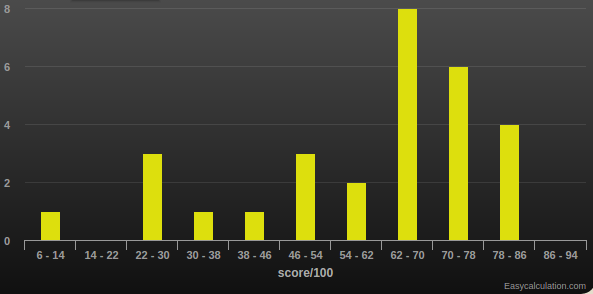
Review session was in Malott 406 (opposite the library), Thursday 1-3 PM.

Book: Beachy and Blair, 3rd edition.

Grading: 25% HW (due Thursdays, in a pile up front at the beginning of class), 25% midterm on March 23), 50% final on Mon, May 22 2:00 PM in Malott 406.

Here are some practice problems for the final, with which you can see the range of topics. (Of course you should also review the ones from the homework!) I may have gone a little overboard but do at least read them, and come to the review sessions with a list of ones you want to hear about.

  • 2.1 #12,18, 2.2 #1,4,8,10,12, 2.3 #4,8,9,14
  • 3.1 #10,11,12, 3.2 #1,4,12,14,16,26,27, 3.3 #3,4,6,14,18
  • 3.4 #1,3,5,11,13,18, 3.5 #1,3,11,17, 3.6 #7,9,12,19,25
  • 3.7 #2,9,14, 3.8 #10,14,20,27
  • 4.1 #10, 4.2 #3,11,14, 4.3 #9,21
  • 5.1 #4,7,12,14, 5.2 #14,23, 5.3 #6,13,20,22
  • 6.1 #6, 6.2 #1,3,4,8, 6.5 #2,11

    • The midterm, with answers, is here. Grades: 70+ = A, 50-70 = B, 30-50 = C. Score distribution:

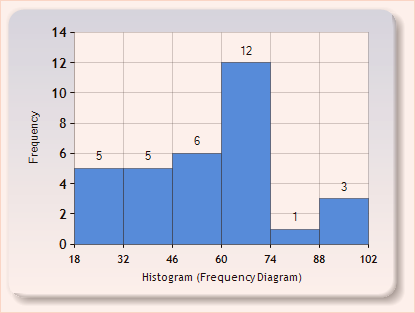
    TA: Theodore Hui

    OH: For me, Tuesday after class in 515 Malott. (It may take a while to get there from class.)
    You can also try the free-for-all on Mondays @12.
    For Theodore, Tuesdays 3-5 PM, in 114 Malott.

    On proofs: As this is a 3000-level course, not everyone may come into the class already knowing how to write and recognize proofs (and non-proofs), but everyone should come out of it with these skills.

    Prerequisites: The principal prerequisites are some fluency with integer arithmetic (e.g. congruences, and the fact that factorization into primes is unique, even if you don't know how to prove that), and real familiarity with linear algebra (e.g. you should get queasy when someone asserts AB = BA without justification).

    It's true in general math classes, but especially true at this level, that they are language classes. Learning a language is hard, and I am likely to use words in it (or more likely, notation) that I've forgotten to define. Speak up and ask me what the notation means! It's 106 times better that we (re)inforce the meaning of some notation for a moment, than that you stew in confusion until the next office hours. This is an important habit for math majors!

    Answers to the homework questions are here and here.

    HW#1 due Thursday 2/2:

  • 1. Prove that the composite of two onto functions is onto.
  • 2. Prove: If f o g is onto, so is f.
  • 3. Prove: If f o g = e o g, and g is onto, then f=e.
  • 4. For each n up to 10, find a graph with exactly n automorphisms. They don't have to be smallest possible, but if you want to prove that your examples are indeed smallest possible, please do!
  • 5. Count the number of partitions of a set with n elements, for n = 1,...,5. Then look up this sequence on the On-line Encyclopedia of Integer Sequences. Example: there are three partitions of the number 3: 3, 2+1, 1+1+1. But there are five partitions of the set {a,b,F}: {a,b,F}, {a,b} U {F}, {a,F} U {b}, {b,F} U {a}, {a} U {b} U {F}.
  • 6. Label the vertices of the left graph by 1-10 and the right by A-J. Find a correspondence between them, giving an isomorphism of the graphs (i.e. taking connected pairs to connected pairs).

    • HW#2 due Thursday 2/9:
  • [Beachy & Blair] 2.1 #1,6,16. 2.3 #1,2,5. 3.1 #2,3,11,12,15.
    • Hw#3 due Thursday 2/16:
  • 1. Recall a relation R ⊆ AxB is any set of ordered pairs, whereas an equivalence relation R ⊆ AxA on A is a relation enjoying reflexivity, symmetry, and transitivity.
  • Given a relation R ⊆ AxA, prove there is a unique smallest equivalence relation E ⊆ AxA containing R.
  • Given R, how would you test whether two elements b,c of A are E-equivalent?
  • 2. Let Dn := {ri, rif : i = 1,...,n} be the rotations and reflections of an n-gon (r for rotate, f for flip).
  • Find all the two-element subgroups of Dn.
  • For each one, list the right cosets by that subgroup.
  • 3. Let G be a group and g an element. Let C = {h in G : hg=gh}. Prove that C is a subgroup. (Which means, check axioms 0,1,2.)
  • 4. Given two elements g,h in G, define [g,h] := g h g-1 h-1, called the commutator of the two. (It's not quite the same thing you would do with matrices, where you could mix addition and multiplication.) It "measures" the failure of g and h to commute.
  • Show (which always means "prove") that the set of commutators satisfies two of the axioms for being a subgroup. (What's much harder is finding an example where the third is not satisfied.)
  • The commutator subgroup is the group generated by the set of commutators. What's the most succinct description of an element of the commutator subgroup? (I.e., it should be tighter than our general description of elements of a subgroup generated by something.)
    • HW#4 due Thursday 2/23:
  • [B & B] 2.2 #5,9. 3.1 #3,13,23. 3.2 #7
    • HW#5 due Thursday 2/30:
  • 1. Let g be an element of a group G, and phi : G -> G be the function taking h |-> h g h-1. In particular the image is "the conjugacy class of g". (Note that this is not the map g |-> h g h-1, in which h would be fixed and g varying, though of course that thing's interesting too.)
  • a. Find all G,g for which this function is a group homomorphism. (Prove you have the exact list.)
  • b. Find all G,g for which this function is 1:1. (Prove you have the exact list.)
  • c. Find all G,g for which this function is onto. (Prove you have the exact list.)
  • 2. Same G,g,phi as above. Show there is a subgroup H such that phi factors as G ->> G/H -> G, where the first map is the usual one, and the second map is 1:1. (Neither are likely to be group homomorphisms. Hint: figure out what this H must be.)
  • 3. Use this to prove that the size of each conjugacy class divides #G.
  • 4. Consider the equivalence relation generated by g ~ g-1, and use it to prove that 2 | #G => there is some element of order 2.
  • 5. Let G be abelian of even order.
  • a. Show that the map Q: G->G, g |-> g2, is not 1:1.
  • b. Show that the set H of elements of odd order is a subgroup.
  • c. Use Fermat's Little Theorem to show that H is in the image of Q. [I was overthinking this.]
  • d. Show that for all sufficiently large powers n, Qn has image H.
  • OPTIONAL. Figure out what Fermat's Little Theorem has to do with anything here.
    • MYSTERY: I've had the dates wrong by a week on the above homeworks since the beginning of the semester... and noone noticed it, and everyone's turned in homework on the "right" day! I'd be more sorry about that, except it apparently didn't matter to anyone.

    HW #6 due 3/9: [BB] 3.8 # 5,6,9,13,17. Compute the sizes of the conjugacy classes in S6; make sure the numbers add up to 6!.

    HW #7 due 3/16:

  • 1. Consider 2x2 matrices of the form

    a b
    -3b a

    where a,b are rational. Show that this set, with its usual (matrix) addition and multiplication, is a field.

  • 2. For p(x,y) a polynomial in x and y, define Rp as the polynomial such that Rp(x,y) = p(y,x). For example if p = x^2 - xy, then Rp = y^2 - xy.
  • a. Show that R(pq) = (Rp)(Rq).
  • b. Use the division algorithm to show that p-Rp is a multiple of x-y. Call this multiple Dp.
  • c. Show that DDp = 0.
  • 3. Define (x choose n), where x is a letter and n is a natural number, as x(x-1)(x-2)...(x-n+1)/n!. This is a polynomial in x with rational coefficients.
  • a. Find and prove a formula for (-1 choose n).
  • b. Show that every polynomial in x of degree at most k is a linear combination of the polynomials (x choose i) for i ranging from 0 up to k.
    • HW #8 due 3/30:
  • [BB] 4.1 #2, 5, 6 (try p=2,3,5 to get the idea), 14. 4.2 #8, 9, 11
    • HW #9 due 4/13:
  • [BB] 5.1 #1,3,9,11, 5.2 #2,3,13, 5.3 #9,11,12
    • HW #10 due 4/20:
  • [BB] 4.3 #3,8,10,14, 5.4 #4,6,8,13
    • HW #11 due 5/4:
  • [BB] 6.1 #1,3,7, 6.2 #2,5, 6.5 #5
    • HW #12 due Tuesday 5/9:
  • [BB] 6.4 #1,5,14, 8.1 #2,6,7