Before jumping
in to some of the more mystifying applications of induction, let’s take
a look at how it works in some more straightforward (but by no means
trivial) examples. Consider the following claim:
The sum of the first n squares
is equal to (1/6)n(n + 1)(2n + 1).
Once again, this is easy enough to check by hand for the first few
values of n:
12
= 1 and (1/6)(1)(1 + 1)(2 x 1 + 1) = (1/6)(2)(3)
= 1,
yes;
12
+ 22 = 1 + 4 = 5 and
(1/6)(2)(2 + 1)(2 x 2 + 1)
= (1/6)(2)(3)(5) =
5,
yes;
12
+22 +32 = 1+4+9 = 14
and (1/6)(3)(3+1)(2 x 3+1)
= (1/6)(3)(4)(7) =
14,
yes. So the claim holds up to the sum of the first 3 squares, but
already things are starting to get cumbersome, and this method of
checking
by hand has no hope of yielding a proof for
all such sums. We
need to
find a better way to go about things.
We might try the same method here
as was used in proving that all squares of even numbers are divisible
by four. Let n be any number, and consider the sum of the first n
squares:
12
+ 22 + 32 + 42
+ ... + (n − 1)2 + n2 .
If we could
somehow add up this sum and show that the result is (1/6)n(n + 1)(2n +
1) then we would be done. Problematically, there is no obvious way to
do this addition (try it and see). We turn to induction.
First comes
the base case n = 1: we must prove that the sum of the first 1 squares
is equal to (1/6)(1)(1 + 1)(2 x 1 + 1). This has already been done,
above, and it was rather easy; it is often true that the base case of
an inductive argument is easy or trivial.
Next comes the inductive
step. We start by making our inductive hypothesis: assume that the
claim is true for n. Our task is to show that it is also true for n +
1. In other words, we need to show that the sum of the first n + 1
squares is equal to
(1/6)(n +
1)[(n + 1) + 1][2(n + 1) + 1],
(1)
which
is just the original formula with n replaced everywhere by (n + 1).
Our
inductive hypothesis amounts to the following equation:
12
+ 22 + ...
+ (n − 1)2 + n2 =
(1/6)n(n + 1)(2n + 1).
Adding (n + 1)
2 to both sides
of the above equation yields
12
+ 22 + ... + (n − 1)2 +
n2 + (n +
1)2 = (1/6)n(n + 1)(2n + 1) + (n + 1)2.
Notice that the left hand side
of this equation is exactly the sum of the first (n + 1) squares! If we
could show that the right hand side of this equation is equal to the
formula labeled by (1), above, then we will have completed the
induction step. Although it is not immediately apparent, the two
formulas in question are in fact equal. The right sequence of algebraic
manipulations reveals this to be so:
(1/6)n(n +
1)(2n + 1) + (n + 1)2 =
(n + 1)[(1/6)n(2n + 1) + (n + 1)]
= (n + 1)[(1/3)n2
+ (7/6)n + 1]
= (n
+ 1) [(1/6)n + (1/3)][2n + 3]
= (1/6)(n + 1)(n + 2)(2n + 3).
Exercise 2
Verify the above equalities.
The reader is invited to verify these
calculations in more detail. Whatever detail is omitted here is done so
for the sake of clarity: there are only so many lines of algebra one
can reasonably be expected to read through before going cross-eyed. The
best path to understanding is to work out the details for your-self,
using the above as a guide.
This completes the induction and therefore
finishes the proof: we have verified that the sum of the first n
squares is always equal to (1/6)n(n + 1)(2n + 1). It is worth noting,
however, that I have left the origins of this formula a complete
mystery. Induction proved quite useful in verifying that the given
formula is the correct one, but how one might come to suspect that
formula in the first place is another issue entirely. I refer the
reader to [1], chapter 2, for a very pleasing exploration of this issue
(the rest of the book is nice, too).
Next I want to give an example of
induction used in a very different situation: to solve a puzzle which
at first glance doesn’t seem to have much use for induction at all. The
puzzle is a tiling puzzle. It asks:
Can a chessboard minus a rook’s
square be tiled with triominos?
What? The first step to solving any problem is understanding the
question, so we start with that. First, a ‘triomino’ is a
two-dimensional figure made out of three equal squares glued together
in the configuration pictured in Figure 1.
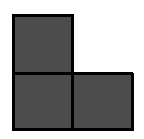
Figure 1: A triomino
A ‘chessboard’ is a more familiar object: it is an 8 x 8 square made
by gluing together 64 smaller squares. Implicit in the question is the
assumption that the squares that make up a triomino are the same size
as the squares that make up the chessboard. A ‘rook’s square’ is any
one of the four corner squares on the chessboard. Finally, the ‘tiling’
that the question asks for is an arrangement of triominos on the
chessboard such that every square of the chessboard (except for one
corner square) is covered by a square from a triomino. No two triominos
are allowed to overlap, and every triomino must be positioned so that
it lies entirely over the chessboard. Can this be done?
The answer is
yes, and if you can get your hands on some triominos (or make some
yourself), after a little experimentation you’ll be convinced of this.
So we can ask a harder question:
Can every 2n x 2n board, minus
a corner square, be tiled by triominos?
The chess board example corresponds to the case n = 3. We can proceed
in the general case by induction in a rather surprising way. That
induction is useful here is perhaps not so surprising, given the nature
of the claim we wish to prove (i.e. we want to prove the claim for n =
1, 2, 3, . . .). But the geometrical aspect of this problem contrasts
sharply with the previous example.
The base case for the induction is n
= 1, so we must consider a 2
1 x 2
1
board with one of the corner pieces
removed and determine whether this can be tiled by triominos. But of
course it can be, since what remains of the board is precisely the same
shape as a single triomino. Once again, the base case was easy.
Now the
induction step. We assume the result is true for n and try to prove it
true for n + 1. This means that we can assume that the 2
n x 2
n board,
with one corner piece removed, can be tiled by triominos. See Figure 2.

Figure 2: A tiling of the 2
n x 2
n
board, minus the upper right corner square.
Note that the actual tiling pattern is not shown; at this point we need
not be concerned with
how
the tiles are arranged, but merely that the
board minus the corner is tiled in
some
way.
How can we use this
tiling, our inductive hypothesis, to obtain the analogous result for a
2
n+1 x 2
n+1 board? Before
reading ahead to the solution, try to play
around with the possibilities for a time. The answer is not complicated
or difficult to understand, but it requires the right flashes of
insight to come up with it.
The first important insight is that the
2
n+1 x 2
n+1 board can be
divided into exactly four 2
n x 2
n
boards by
cutting it vertically and horizontally down the center lines. Our
inductive hypothesis tells us that we know how to tile such boards with
triominos, minus a corner square. So let that be done.
The second
insight is best provided in picture form: we glue the four quarters
back together in the configuration shown in Figure 3. This leaves one
corner square (the one in the upper right) untiled, along with three
central squares. But look! The three central squares that are untiled
have been glued back together in exactly the shape of a triomino!
Therefore, with the addition of one extra triomino in that conspicuous
space, we have managed to completely tile the 2
n+1 x 2
n+1 board, minus
the square in the upper right corner. This completes the induction and
finishes the proof.
Before moving on, it is worth noting a small
corollary to the result we just proved. Since each triomino is composed
of exactly three squares, any area that can be tiled with triominos
must consist of exactly 3k squares, where k is the number of triominos
used in the tiling.
Exercise 3
Show that the converse of this statement
is false. That is, show that there are areas consisting 3k squares, for
some natural number k, that cannot be tiled with triominos.
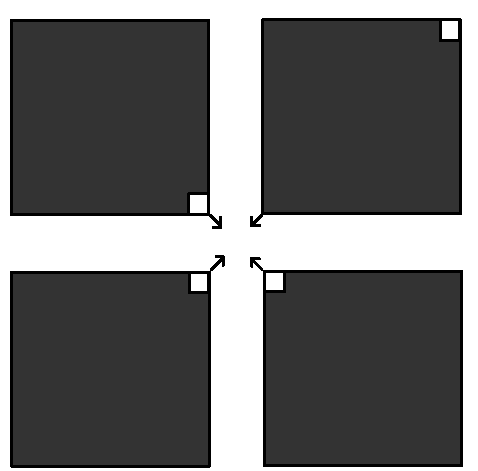
Figure 3: Gluing the four quarters back together.
The number
of squares in a 2
n x 2
n
board is 2
n x 2
n = 2
2n
. So a tiling of this
board minus a corner square is a tiling of an area consisting of
exactly 2
2n − 1 squares. We can therefore deduce
that 2
2n − 1 = 3k
n for
some k
n (the subscript n is included to indicate
that the number k
n
depends on n). This isn’t the most interesting result in the world, but
it is not exactly obvious and we get it for free from our tiling proof.
Exercise 4
Prove this result directly. That is, prove by induction on n without
reference to tilings that for all natural numbers n the number
22n − 1 is divisible by 3.
Exercise 5
Find an explicit formula for kn in terms of n.
(Hint: use the tiling proof or your answer to the
previous exercise to guess the formula and then verify it.)