
Transforming a triangle
In the following activity we will study the symmetries of an equilateral triangle, and this will be our first example of what we will later call a group -- a symmetry group, actually.
The main player in this act is an equilateral triangle: a triangle whose 3 sides are all of equal length. Let us get started by drawing such a triangle and then by naming all the corners with letters A, B and C. This way, it will be easier to refer to the different parts of the triangle in what follows.
Let us now consider a certain set of transformations. One could get into more complicated -- and more correct -- definitions of what we mean by that, but here, we just mean that we think of the triangle as a phisical object sitting on a piece of paper on the desk. As such, we can move it around the page, rotate it, even maybe stretch it if we assume that the sides are made out of a "rubbery" material.
To be a little more explicit, we consider and restrict ourselves to what is called affine transformations. let us list the kind of transformations of the triangle we are allowing ourselves to play with. One could obviously think of even more ways to "warp" the triangle, but the following will be good enough for us.
Note that in all the diagrams, the dotted triangle is the original triangle, while the solid one is the one after the transformation.
First, we can scale the triangle up and down:
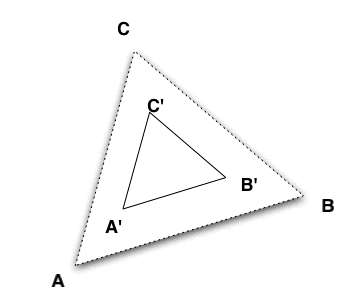
Then we can translate it, or move it around:

But we can also rotate it, given a center of rotation, an angle and a direction:

Also, we can pick a line on the page, and draw the reflection of the triangle with respect to that line:

Finally, we can do the following. Without getting into too many details, let us just say that we can move the vertices A, B and C to other positions and connect the new points to obtain a new triangle. We will not be considering this kind of transformation in what follows and you will be able to see why. We are only mentioning these here for the sake of completeness. Note that this kind of transformation encompasses the previous ones.

There are obviously infinitely many transformations of these sorts. For example, considering the rotations alone, it is clear that one has infinite possible choices for the rotation center and the angle.
Something interesting happens nevertheless when we focus on the special subset of these transformations that leave the equilateral triangle invariant, meaning that the image of the new triangle after the transformation and the image of the original triangle overlap. In other words, after the transformation the new triangle is such that its vertices A', B' and C' all lay over a different original vertex, but we don't have necessarily A=A', B=B' or C=C'.
We call these transformations the symmetries of the triangle and we will focus on them in what follows.
Symmetries: A taste of group theory
Let us thus list all the transformations that leave the triangle invariant, going through the list we gave earlier.
- Scaling:
- Say we scale the triangle by a factor K with center the center of the triangle and so the length of the sides is multiplied by k. More specifically, call the center of the triangle O, then for each vertex of the triangle, trace the line joining O and that vertex and call L the distance between O and the vertex. Finally, place a new vertex on the line at a distance K x L away from O. Now do the same thing for the other two vertices. Here is a picture that shows the process:
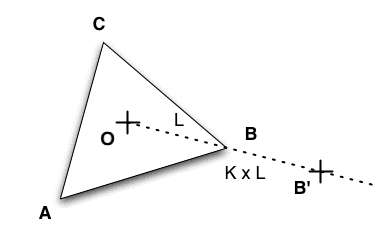
Looking at the picture, it is clear that the only way for the new triangle and the original triangle to overlap is to take K = 1: We are making the new triangle to be exactly the original one. In other words, we are not doing anything!.
While this may look insignificant at first, the existence of a not doing anything transformation turns out to be a very fruitful idea and also a necessary one for the development of group theory. It is so important it even gets a fancy name: the trivial transformation.
- Translations:
- The translate of the triangle is obtained by shifting each vertex by a fixed displacement called the translation vector. Looking at the picture we had before, it is clear here again that the only way for the new triangle and the old triangle to overlap is to take the displacement to be the "no displacement" translation vector. In other words, here again, the only way to get a symmetry of the triangle is to apply the not doing anything translation, i.e. the trivial translation!
So far, we have annalyzed two of the main types of transformations and the only symmetry we have found is the trivial transformation. Notice that the not doing anything translation and the not doing anything scaling are the same transformation: leave the triangle exactly as it is.
Let us look at this trivial transformation a little closer. Suppose we translate the triangle by some none emtpy vector, say "to the left". We get a new triangle that does not overlap the old one, and hence this is not a symmetry of the triangle. Now, translate the newly obtained triangle back to the original position. The triangle we get now overlaps the original triangle and this is a symmetry of the triangle. Let us rephrase this in words we will need later on. We moved the triangle "to the left" and then back "to the right". This is a transformation of the triangle, that happens to be described using two well known steps, and we call it the composition of those two transformations. Notice that while we used two translations in this example, one can obviously compose any two transformations (example: a rotation then a translation, etc...).
The composition of two general transformations can be anything -- any transformation that is! Indeed, the only thing we know for sure is that when we compose two transformations, i.e. apply them one after the other in order, we will always get a transformation, but this transformation can bear very little ressemblence to the two original ones sometimes.
In some cases though, the composition of two transformations yields the trivial transformation: the two transformations cancel each other out! This is very similar in idea to adding 3 to a number and then substracting 3 to the result: x + 3 - 3 = x + (3 - 3) = x + 0 = x.
 Suppose we compose two transformations, T1 first then T2, and suppose also that we get the trivial transformation. An example of this situation would the two translations mentioned earlier: translate "to the left" and then "back to the right". A natural question that arises is whether we still get the trivial transformation if we compose the transformations in reverse order? In this translation example, the answer is clearly yes. Is always the case when we compose two transformations? Suppose we compose two transformations, T1 first then T2, and suppose also that we get the trivial transformation. An example of this situation would the two translations mentioned earlier: translate "to the left" and then "back to the right". A natural question that arises is whether we still get the trivial transformation if we compose the transformations in reverse order? In this translation example, the answer is clearly yes. Is always the case when we compose two transformations?
One way to answer this question is to list all possible symmetries -- as we're doing -- and then compose them and see what happens. This obviously not an appealing solution. Algebra and its framework for Group theory will allow us to give a very general answer with much less sweat.
- Rotations:
- It is clear that if we are looking for symmetries for the triangle, all we have to do is look at rotations with center the center of the triangle. By center, in this case, we mean the point that is at an equal distance from all 3 vertices. Indeed, a rotation preserves lengths. The image A' of A under a rotation of center D will be at a distance DA' such that DA = DA'. But now because we are looking for a symmetry, that image A' can only be A, B or C. This proves that the center of the rotation has to be equidistant to A, B and C.
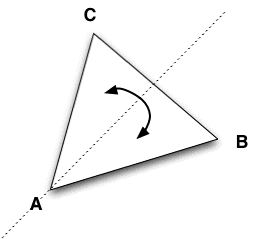
Now which ones of those rotations are indeed symmetries of the triangle. Let's look at the following animation:

As we increase the rotation angle, new B keeps getting closer to old C, and new A and C keep getting closer to old B and old A respectively. When B reachs old C for the first time, A and C reach old B and A for the first time as well, and we find a symmetry.
How do we find out what exact rotation angle gives that symmetry? Well, the rotation takes each corner of the triangle to the next one in a counter-clockwise order. So the rotation angle is nothing but the angle between two adjacent corners as viewed from the center of the triangle: 2 Pi / 3 radians, or in degrees: 360* / 3 = 120*. Let us call this symmetry R1.

If we keep rotating the triangle counter-clockwise, we find two other symmetries.
 Make those two symmetries explicit by finding the rotation angles. Let us call these symmetries R2 and R3, where R2 is obtained by rotating by a smaller counter-clockwise angle. Make those two symmetries explicit by finding the rotation angles. Let us call these symmetries R2 and R3, where R2 is obtained by rotating by a smaller counter-clockwise angle.

- What is special about R3? Reprhase this using the trivial transformation language.
- Let us look at the first symmetry R1 we have found: we rotate the triangle around its center by 120* counter-clockwise. What happens when we compose R1 and R1, that is to say we do R1 twice in a row. Compare the composition symmetry with R2.
- What happens now if we compose R1 three times in a row? Compare with R3.
- What is the composition R1 then R2? How about R2 then R1? are they the same?
- Rephrase the previous answer in terms of transformations that cancel each-other out and show how this gives another example of pairs of transformations that cancel each-other out no matter what order we compose them in.
 Suppose now we rotate the triangle 120* clockwise
Suppose now we rotate the triangle 120* clockwise
- Show that this is also a symmetry of the triangle. Call it R4.
- If we compose R4 with R1, we get the trivial transformation because that ends up rotating the triangle 120* counter-clockwise back to its original orientation. But we already know that composing R1 and R2 also give the trivial transformation. What kind of relationship is there between R2 and R4?
This is similar to the following: Suppose 3 + x = 0. But also 3 + (-3) = 0. With numbers, you know this means x = -3. In other words, given a number, there is one and only one other number that cancel it when we "compose" them with pluses.
Whether this is true or not for symmetries is still out of our grasp. We will be able to answers questions like these when we introduce groups and their language.
- Reflections:
- Let us look at reflections now. Because there are only 3 corners to the triangle, the reflection axis has to go through one of those corners to get a symmetry. Indeed, each corner has to go to a corner and we cannot have two coners going to the same corner after the reflection -- that is just impossible.
Say the axis goes though A now, then to get a symmetry we must have that B and C are exchanged under the relection. This prooves that the reflection axis of a symmetry goes through segment [BC] and interesects it a right angle.
 Show that in that case that the reflection axis goes through A and the middle of segment [BC] -- you can use the fact that the triangle is equilateral and hence all 3 corners make 60* angles. Show that in that case that the reflection axis goes through A and the middle of segment [BC] -- you can use the fact that the triangle is equilateral and hence all 3 corners make 60* angles.
In summary, we have found 3 reflections that are symmetries:


Call these XA, XB and XC depending on whether A, B or C lies on the axis
So far, it looks like we have found the trivial transformation, 4 rotations and 3 reflections, and hence at least 8 symmetries. We said at least because we haven't studied the compositions of reflections and those of relections with rotations: those are all symmetris and could new ones we haven't listed yet.
The truth is a little different though. We have already seen when we studied rotations that R3 was trivial and R4 = R2 and hence we only have 2 rotations really, not counting the trivial one.
Also, R2 was nothing but the composition of R1 with itself twice, and R3 the trivial rotation was also nothing but R1 composed three times with itlself.
We can write this as:
R2 = R1 @ R1 and R3 = trivial = R1 @ (R1 @ R1)
where X @ Y means we compose X and Y by applying Y first then X second. The parenthesis will turn out to be not needed here but we will talk about them more in depth in the later sections.
Let us now look at compositions of reflections then. When we combine a reflection with itlself we get the trivial transformation by definition of a reflection:
XA @ XA = XB @ XB = XC @ XC = trivial
What happens now when we compose, say, XA with XB (where XB always refers to the reflection corresponding to the original B vertex):

We see that the composition is nohting but R2! In other words, with our notation:
XB @ XA = R2
 Explicit the compositions XC @ XA and XC @ XB = R2 as we did above. Explicit the compositions XC @ XA and XC @ XB = R2 as we did above.
Finally, let us look at the composition R2 @ XA:
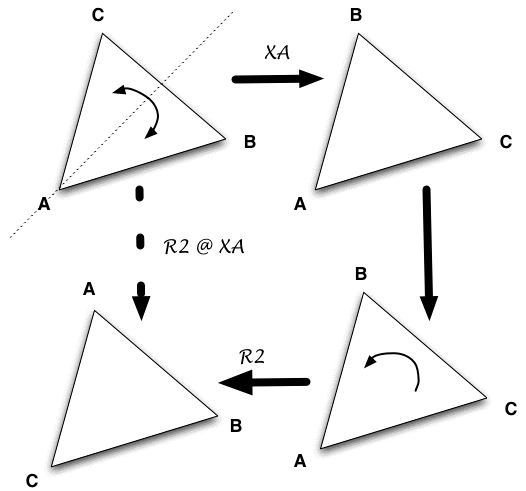
This shows that:
R2@ XA = XB
 Find out what XA @ R2 is using similar diagrams. Show that XA @ R2 = XC Find out what XA @ R2 is using similar diagrams. Show that XA @ R2 = XC
and that in this case:
XA @ R2 ≠ R2 @ XA
We say that those two transformations do not commute: the order in which we compose them matters.
Putting it all together
So far we've looked at an equilateral triangle and we have listed all its symmetries. Doing so we discovered the following properties of those symmetries:
- The symmetries form a set -- we were able to list them all
- Given two symmetries, we were able to compose them in a natural way -- remember, they are just special transformations! -- obtaining another symmetry.
- There is a special symmetry, the trivial one, that is important because of the following point.
- Given any of the symmetries, there is always another symmetry that cancels it out to the trivial symmetry by composition. For example R1 and R2 = R1 @ R1 cancel each other out. We do not know wether such a canceling symmetry is unique or not yet.
- We were able to find generators for the symmetries, although we did not phrase it that way. We showed (partially) that by doing various compositions of R1 and XA, we could cook out all of the other transformations. We say that R1 and XA are generators for the symmetries.
These properties are the heart to the notion of a Group as we will see later. Brilliant people realized that many sets of mathematical beings shared these properties as well, even if they weren't directly related to the symmetries of a particular object.
By studying where these properties lead to in the abstract setting of algebra, they were able to answer a lot of question -- just like the determining whether canceling symmetries are unique or side dependent -- in great generality.
Furthermore, they were able to find new deep properties of these sets that were not obvious in their first description, and deep connections with other areas of mathematics.
Before moving on to the abstract definition of a group, we will spend some time looking at other sets sharing the properties cited above.
 Show that R1 and XB are also generators. Same thing with XA and XB. Show that R1 and XB are also generators. Same thing with XA and XB.
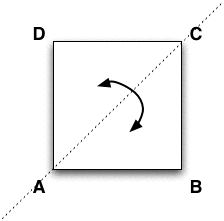
 Consider the following square: Consider the following square:

- Show that the symmetries of the square are of 3 basic types: rotations around the center of the quare by multiples of 45*, reflections across axes joining two opposite corners and reflections across axes joining the middle points of two opposite sides:

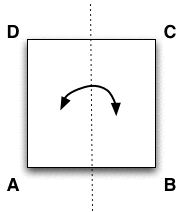
- List all of those symmetries, and calculate a few compositions.
- Using the answers to the previous question, determine a set of generators for the symmetries of the square.
|
|