So far, given a process modeled as a Markov chain, we are able to calculate the various probabilities of jumping from one state to another in a certain given number of steps. This was given by taking successive powers of the transition matrix and reading a coefficient in the result matrix.

For example, we are to able to calculate the probability for Little Ricky to reach state 5 in 2 steps starting in state 1, or in 3 steps starting in 1, or even in 4 steps starting in 1.

What we are still lacking though, is the ability to answer questions like this: forgetting about how many steps it takes her to do it, what is the probability for Little Ricky to ever reach state 5 starting in state 1? While it might be possible to guess what the answer should be in this case, more complicated examples might require a new kind of approach and this is what we will focus in this section. Rather than giving a general statement we develop the idea using a simple example.

Let us create a new maze by describing it using the following graph:
The missing arrows indicate a zero transition probability. For example, state 1 and 4 don’t have any arrows coming out them. We call such states absorbing states. This simply means once the process reaches one of those states, it stays in them forever. In this example, rooms 1 and 4 are two exits. Once Little Ricky leaves the maze, she stays ”out” forever – or till the end of the experiment, that is. Non-absorping states are also called transient.

In the following, we show how to calculate the average time it takes Little Ricky to get to one of the exits (rooms 1 and 4) and the probability that she exists through room 4. More precisely:

Definition

Define πi to be the probability of ever reaching state 4 starting for state i, and τi to be the average number of steps required to get from state i to either state 4 or state 1. Finally, we will write {i → j } to denote the event {Little Ricky reaches state j starting from state i}.

1. Absorption Probabilities

Let us first focus on π_i ’s. Clearly, π₁ = 0 as she can’t reach state 4 starting from state 1. Also τ₁ = 0 as 1 is one of the target states: it takes Little Ricky no steps to get from 1 to either 1 or 4.



Now suppose she starts in state 2. We break the event {2 → 4} apart depending on whether she first jumps to state 1 or 3. These two events being disjoints, we get that:

We first simplify this into:

Finally, using the transition probabilities and the independence of the transitions in a Markov chain, this becomes:
π₂ = p₁₂ π₁ + p₃₂ π₃ = (1/2) π₁ + (1/2) π₃ = (1/2) π₃

2. Average Time to Absorption

To calculate the average time to absorption we need to remember that in probability theory, the average of a random variable is defined as the expectation of that variable:

Definition

The expectation of random variable X that can take values 1, 2, … , k (k can be infinity, but mathematical care is needed to is defined the sum) as

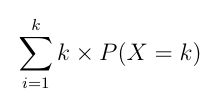
Getting back to our original problem, we want to calculate the average time to get to rooms 1 or 4.

Let us write P (i → E in k) for the probability of reaching state 1 or 4 in k steps starting from state i and let us try to find an expression for the average time τ₂ it takes Little Ricky to find one of the exits starting in room 2. By the definition, we have:
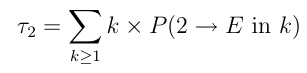
Here again, we split those probabilities depending on whether the first step is a step towards state 1 or 3, and use the same kind of trick we used many times before:


In this section we tried to show how one can solve absorption problems explicitly when the graph of the Markov chain is small enough to make the calculations feasible by hand. A more general treatment of this kind of problems requires tools from linear algebra beyond the scope of this introduction.