|
6. The complex half-plane model for the hyperbolic plane
First, review complex numbers! From now on we use the properties of complex numbers!
The model that we start with is called the the upper half-plane model and it is defined to be:
This simply says that we consider all the complex numbers that have the imaginary part strictly positive, i.e. if 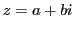 , then , then 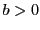 . .
The notion of angle in
 is the one inherited from is the one inherited from
 , so the angle between two curves is the angle between their tangent lines. , so the angle between two curves is the angle between their tangent lines.
Before we prove anything, let's do some warm-up exercises.
Exercises
Exercise 1
Express the equations of the Euclidean line 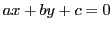 and the Euclidean circle and the Euclidean circle
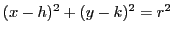 in terms of the complex coordinates in terms of the complex coordinates 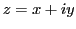 . .
Exercise 2
Let
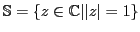 be the unit circle in the complex plane. Let be the unit circle in the complex plane. Let 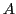 be a Euclidean circle in the complex plane, with Euclidean center be a Euclidean circle in the complex plane, with Euclidean center
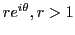 and Euclidean radius and Euclidean radius 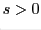 . Show that . Show that 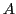 is perpendicular to is perpendicular to
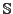 if and only if if and only if
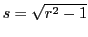 . .
You may wonder how this hyperbolic world looks like in this model. A good way to imagine it is to see how lines look like in this new world.
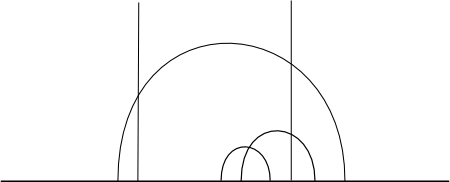
Hyperbolic Lines
There are two seemingly different types of hyperbolic lines, both defined in terms of Euclidean objects in
 . One is the intersection of the half-plane with a Euclidean line in the complex plane perpendicular to the real axis . One is the intersection of the half-plane with a Euclidean line in the complex plane perpendicular to the real axis
 . The other is the intersection of . The other is the intersection of
 with a Euclidean circle centered on the real axis with a Euclidean circle centered on the real axis
 . Here is a picture of hyperbolic lines: . Here is a picture of hyperbolic lines:
Figure 1:
Hyperbolic lines in
|
 |
Since the only difference between non-Euclidean and Euclidean geometry is the fifth postulate, the first four should hold. Using just our definition above, we should see that those four postulates hold. The proof is very tedious, so we will only show the first one: there should exist one and only one hyperbolic line passing through any pair of distinct points. Let's see how this follows from our definition:
Proposition 1
For each pair 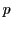 and and 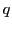 of distinct points in of distinct points in
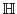 , there exists a unique hyperbolic line , there exists a unique hyperbolic line 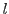 passing through passing through 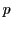 and and 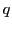 . .
PROOF.
This is a typical existence and uniqueness problem. We will first show that such a line exists, and then that it is unique. We divide the proof into two parts: existence and uniqueness.
Existence
There are two cases to consider. Suppose first that
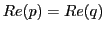 . Then the Euclidean line . Then the Euclidean line 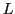 given by the equation given by the equation
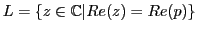 is perpendicular to the real axis and passes through both is perpendicular to the real axis and passes through both 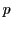 and and 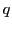 . So the desired line is . So the desired line is
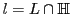 . .
Suppose now that
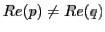 . As the Euclidean line through . As the Euclidean line through 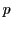 and and 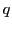 is no longer perpendicular to the real line, we need to construct a Euclidean circle centered on the real axis and passing through the two points. is no longer perpendicular to the real line, we need to construct a Euclidean circle centered on the real axis and passing through the two points.
Denote with 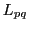 the Euclidean line segment joining the two points, and let the Euclidean line segment joining the two points, and let 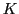 be the perpendicular bisector of be the perpendicular bisector of 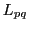 . Then (and this you should know from Euclidean geometry), every Euclidean circle that passes through . Then (and this you should know from Euclidean geometry), every Euclidean circle that passes through 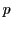 and and 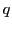 has its center on has its center on 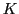 . As . As 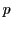 and and 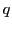 have non-equal real parts, the Euclidean line have non-equal real parts, the Euclidean line 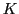 is not parallel to the real axis, so is not parallel to the real axis, so 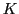 intersects the real axis at a unique point intersects the real axis at a unique point 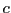 . .
Let 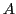 be the Euclidean circle, centered at this point, with radius be the Euclidean circle, centered at this point, with radius
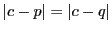 (the two are equal, since the circle passes through both points) (see figure). So we have the line, (the two are equal, since the circle passes through both points) (see figure). So we have the line,
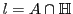 . .
Figure 2:
Constructing a hyperbolic line
|
 |
Uniqueness
The uniqueness of the line follows from the uniqueness of the Euclidean lines and the Euclidean circle. The proof of the first postulate is complete. 
Note that since we have chosen the underlying space for this model of the hyperbolic plane to be contained in the complex plane, we can use whatever facts about Euclidean lines and Euclidean circles we already know to analyse the behaviour of hyperbolic lines.
For example, if 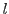 is the hyperbolic line in is the hyperbolic line in
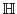 passing through passing through 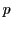 and and 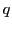 , we can express , we can express 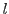 explicitly in terms of explicitly in terms of 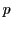 and and 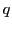 . Like we saw above, if the two have the same real parts, then . Like we saw above, if the two have the same real parts, then
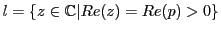 . For the second case, do the following exercise: . For the second case, do the following exercise:
Exercise 3
Let 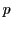 and and 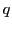 be distinct points in be distinct points in
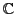 with non-equal real parts, and let with non-equal real parts, and let 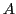 be the Euclidean circle centered on be the Euclidean circle centered on
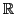 and passing through and passing through 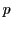 and and 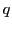 . Express the Euclidean center . Express the Euclidean center 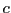 and the Euclidean radius and the Euclidean radius 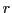 of of 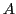 in terms of in terms of 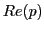 , , 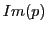 , , 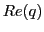 , , 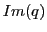 . .
Hyperbolic geometry behaves very differently from Euclidean geometry in
 , even though it is expressed in terms of the latter. , even though it is expressed in terms of the latter.
Definition 1
Two hyperbolic lines in
 are parallel if they are disjoint. are parallel if they are disjoint.
Now we can see a first difference: in Euclidean geometry, parallel lines are equidistant, and so there is only one parallel through a given point to a given line, but in hyperbolic geometry things are completely the opposite - there are infinitely many distinct parallel lines through a given point to a given line.
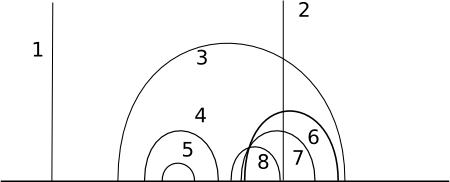
In the figure below you can see how parallel lines look in our model of the hyperbolic plane: lines 1, 3, 4, 5, 6 are parallel, but 2, 3, 6, 7, 8 are not. Try to find all the pairs of parallel lines.
Figure 3:
Several parallel hyperbolic lines
|
 |
You may wonder how polygons, circles and other figures look in hyperbolic geometry. The half-space model is not very good to visualise these objects, it is mostly used for computation or proving different properties (even if there are different models, the properties are the same for all, since they all describe the same concept, hyperbolic geometry). This is the reason why the next model, the Poincaré disk, is used for visualisation.
|


