Dutch auction
It is important to point out
that eBay uses the term "dutch auction" differently. eBay's
Dutch auction is a multi-unit auction for several
identical goods to be sold simultaneously to potentially multiple
bidders.
This auction is the converse of the English auction. The auctioneer
calls prices in a decreasing way starting from a high price. The
auction ends when one bidder accepts the price. This type of auction,
rather uncommon, is used, for instance, for selling cut flowers in the
Netherlands, fish in Israel and tobacco in Canada.
We will see that the main difference between the equilibrium in the
Dutch and English auctions is that in the Dutch auction the equilibrium
strongly depends on the bidder's guess about the others decision rules,
while in the
English auction
the bidder's strategy does not depend on what he/she believes about
his/her rivals bids. To better understand this difference, it is
important to define the concept of
Bayesian Nash Equilibrium.
Activity 1
Organize a Dutch auction with two of your friends. Assume that their
valuations satisfy the same properties as the ones listed in the
example presented at the beginning of the
previous
lesson. You will act as the auctioneer and they will act as
two bidders. Explain the rules of the game to the bidders in a clear
manner. What is the outcome of the auction? How would the outcome have
changed if some of the hypotheses A1-A4 are relaxed?
Bayesian Nash Equilibrium
For simplicity we will introduce the concept in the context of auctions
satisfying hypotheses A1-A4 of
lesson
1. A generalization to the general case of games with
incomplete information is natural. Suppose that there are
N
bidders in an auction, with valuations
v1,...,vN.
The believes of bidder
i about other bidders'
valuations are independent of
vi
and they are the same for all bidders. Let's denote by
V-i
the set of all possible combinations of valuations of all bidders
except for bidder
i. A
Bayesian
Nash Equilibrium is a set of
strategies,
(s*1,...,s*N),
that specify the actions of the players given their own valuations and
such that for each bidder
i,
the strategy s*i(vi)
is on average the best response, assuming i's
rivals play according to (s*1,...,s*N).
In other words
s*i(vi)
solves the maximization problem (see figure)
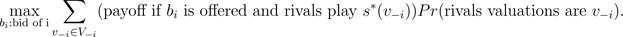
This definition might appear to be rather complicated because of the
notation. However, a careful analysis of this concept reveals that it
is a natural generalization of the concept of
Nash
equilibrium in games with complete information to games with
incomplete information. Summarizing,
in
a Bayesian Nash equilibrium of an auction each bidder chooses his/her
best bid given his guess about the decision rules being followed by
his/her rivals (correct guess in equilibrium).
Activity 2
Explain why bidding their own valuation is a Bayesian Nash equilibrium
in a second-price sealed-bid auction (see
previous
lesson).
It is easier to understand the outcome of a Dutch auction by studying
the first-price sealed-bid auction.
The first-price sealed-bid auction
This kind of auction has the same structure than the second-price
sealed-bid auction described in the
previous
lesson, except that in this case the winner of the auction
pays his/her own bid for the item. Unlike the English auction, bidders
never see their rivals' bids and can only submit one bid. This type of
auctions are commonly used for selling mineral rights to U.S
government-owned land, and sometimes used for selling artwork and real
estate property. Also, their analysis can be used to understand
tendering of government procurement contracts.
Activity 3
- Organize a first-price
sealed-bid auction with two of your friends.
Assume that their valuations satisfy the same properties as the ones
listed in the example presented at the beginning of the previous lesson. You will act
as the auctioneer and they will act as two bidders. Explain the rules
of the game to the bidders in a clear manner. What is the outcome of
the auction? How would the outcome have changed if some of the
hypotheses A1-A4 are relaxed?
- In a first-price sealed-bid
auction, why is submitting bidders' own
valuation is not an equilibrium anymore?
Example
Suppose that there are only two bidders in a first-price sealed-bid
auction, labeled
i=1,2. The two bidders'
valuations,
v1, v2
are independent and
uniformly
distributed on [0,1]. We claim than in this case submitting
vi/2
is a
Bayesian Nash equilibrium for each player
i
(see figure below). For instance, for player 1 we have to check that
v1/2
maximizes the quantity
(v1-b1)Pr(b1
> v2/2),
over all possible bids
b1.
This last expression is the expected payoff for player 1 if player 2
has the same bidding rule. From the definition of the
uniform distribution this
quantity is equal to
(v1-b1)2b1,
for
b1≤ 1, and
(v1-b1)
for
b1>1.
Activity 4
Complete the reasoning initiated above. It could help to graph (v1-b1)2b1
as a function of b1 for some
values of v1 in [0,1].
Hence in this case the bidder with the highest valuation wins the
auction and pays a price equal to
v(2)/2
(see the definition of
order
statistic). It turns out that the expected value of this
quantity is 1/3, just like in the second-price sealed-bid auction. This
is a general result that we will present in the
next lesson.
We stated before that it is easier to understand the outcome of a Dutch
auction by studying the first-price sealed-bid auction. This is a
consequence of the following theorem.
Theorem
The Dutch auction yields the same outcome as the first-price sealed-bid
auction.
It is quite easy to see why this is the case: in each auction the
bidder faces the same situation, he/she has to decide how high to bid
without knowing the other bidders' decisions, and if he/she wins,
he/she pays a price equal to his/her own bid. Observe that this
conclusion does not depend on hypotheses A1-A4.