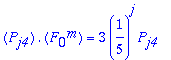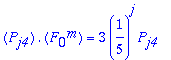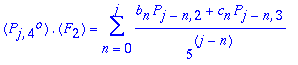Polynomials on the Sierpinski Gasket with a Boundary Singularity
When there exists a singularity at one of the boundary points of the Sierpinski Gasket, one can find a four-dimensional space of harmonic functions across the Gasket. Two dimensions correspond to functions symmetric about the point of singularity, while two dimensions correspond to skew-symmetric functions. In 2002, Jonathan Needleman and Po-Lam Yung were able to create "monomials" analogous to x^n/n! for use in power series for three dimensions. Please go here to read up on this. Each monomial is actually an n-harmonic function on the Gasket. These families corresponded to the removable singularities at the boundary point. The first two are symmetric, while the third is skew-symmetric. If you would like to read more about their work, you can go here
For my work this summer I investigated the fourth and final family of monomials. This family corresponds to the only non-removable singularity. In fact, for the harmonic function, the gasket has a pole at the point of singularity. We focus on the F2 contraction of the gasket, which contracts down towards the lower right corner, i.e. towards q2. The lower left triangle will be a mirror reflection of this while all subsequent upper triangles will be constant multiples. The equation which governs this relation between contractions moving towards the boundary singularity at q0 is:
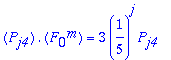
We were able to construct the F2 contraction of the gasket out of the Pj3's and Pj2's with appropriate coefficients according to the following equation, where the P2's and P3's are centered at q1, while P4, as we can see, is centered at q0.
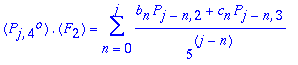
By using the gluing requirement of normal derivatives at a point as well as the above relation between points moving towards the singularity, I was able to create a MAPLE program which could calculate arbitrarily many b's and c's. To see a list of the b and c values up to j=50, go here. This program is available here. I then calculated the ratios of successive coefficients and these both converged to a very interesting figure: -279.429... , which is five times the first eigenvalue in the 5-series, a value that came up in work with the Finite Element Method. You can learn more about that here.
Once I had the b and c coefficients, I was able to find the values at any point on the F2 contraction of the Sierpinski Gasket. For the sake of time and computer memory I only calculated the boundary points and midpoints on this triangle, i.e. V1 on the F2 of SG triangle. From this point on, when referring to points, I will be referring to them on the F2 subtriangle, rather than the entire graph. So V1 = {q0, q1, q2, q01, q12, q02} on the F2 subtriangle. Going clockwise from the top point, the points are q0, q02, q2, q12, q1, q01.
Because the entirety of the Sierpinski Gasket in this context is skew-symmetric, the point q1 always has the value 0. Using these two programs, Program 1,Program 2, I was able to calculate the values on the other 5 points. What was of special interest was the set of ratios of the values of a point from level j-1 to level j. Both the values of the points and their ratios can be seen here. These ratios quickly converged to very familiar numbers. The ratio at q0 converged to -3389.303175, at q01 and q02 it converged to -279.429137, and at q12 and q2 it coverged to -677.860635. All of these values are familiar Dirichlet eigenvalues on the gasket. -279.429137 is, as stated above, 5 times the first eigenvalue in the 5-series. -677.860635 is the first eigenvalue in the 6-series, and -3389.303175 is 5 times the first eigenvalue in the 6-series. These are all related to the finite element work mentioned above. Also, we noticed that the values at q01 and q02 were equal and opposite in addition to shrinking at the same rate. Thus, there was an additional level of skew symmetry in this subtriangle. This meant, because of the similarity equations described above and the symmetry, that all smaller right subtriangles approaching the singularity would possess this same skew symmetry, as well as all left ones, since the left triangles will be mirror reflections with opposite signs.
Using code downloaded from Jonathon Needleman's website and a program I created to manipulate the data created there, I was able to produce graphs of the F2 subtriangle of the gasket. You must fully run all of Needleman's code, including the tutorial, before running mine. Below are all of the pictures of multiharmonics on the F2 subtriangle we have been able to generate so far for the 4th family.
Pj4 Pictures
Based on our data for the values and ratios, we were able to conjecture about what the eigenfunction about the entire gasket would like like. A picture of that conjecture is below.
main