It would be nice if some argument for a game (like chomp) works for other games (like chess). Let’s generalize slowly (chess is not included yet):

Consider all games which
1) will finish in a finite number of moves
2) has one winner and the other is the loser
Then we claim that: either the 1st or 2nd player has a winning strategy.

Proof: For all games that are finished in at most one move, either there exists or there does not exist a move that makes 1st player win, so the claim holds. For all games that are finished in at most two moves, making a move results in a game of at most one move, after which either the 1st or 2nd player has a winning strategy by the first sentence of the proof. So either there exists a move that makes it into a game of at most one move such that the 2nd player has a winning strategy or there isn’t, so the claim is true for games with at most two moves. Keep on inducting and we are done.

What happens if we change 2) to allow for draw? Then is it true that either the 1st or 2nd player has a non-losing strategy?

Let’s simplify by assuming (though not necessary)
3) there is only finite number of choices for each move.

Then we can draw a game tree and put 1, 0 or -1 (called the payoff) at the end of each branch representing 1st player win, draw or 2nd player win, respectively.

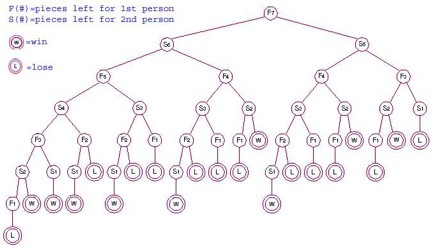
Activity 5

1. Who has a non-losing strategy for the game tree above? (L is -1, W is 1; the game is a variation of nim. More detail here)
2. How about a much bigger game tree, do you have an algorithm to do it in general?

The analysis here is similar to that in game theory. (The scenario in game theory involves players moving simultaneously, so probability is needed to mix up several strategies to achieve optimal average payoff in the long run; then a non-losing strategy is not guaranteed.)

Suppose the game ends after n moves. Since there are only payoffs at the leafy end of the tree, which only helps you decide during the n-1 move to the n move, it’s hard to decide how to make the first move. It would be nice to have payoffs everywhere in the tree. [We can move the existing payoffs (after n moves) up to get “payoffs” after n-1 moves, assuming the player playing that move plays optimally. So for example, if it’s the 1st player to move starting at a point after n-1 moves and the resulting payoffs are 0 and 1 after that move, the “payoff” before that move is 1. But if it’s the 2nd player, the “payoff” before that move is 0. Repeating this for points after n-2 moves, then n-3 moves and etc., every branching point will have a “payoff”. ]

Ex: Given a position, what does its “payoff” means?

[If it is 1, then if the 1st player move next, he can move to “payoff” 1 (but not higher), and if the 2nd player move next, he can move to “payoff” 1 (but not lower). So 1st player can get at payoff at least 1 because he can keep moving to a point with “payoff” at least 1, but if 2nd player didn’t screw up, it will be 1 and not higher. Similarly, 0 means, depending on who moves, the 1st (or 2nd player) can move to “payoff” 0 but not higher (or lower).]

The “payoff” at the starting position is called the minimax because it is the best payoff that player 1 can achieve with player 2 trying best to minimize it.

So what does this say about the existence of non-losing strategies? If minimax is 0 or 1, that means no matter what player 2 does, player 1 will not lose (similarly for player 2 if minimax is -1 or 0).

Aside: For 2 players moving simultaneously, the minimax theorem claims that the minimax exists and can be achieved in the long run. Also the minimax will be a Nash equilibrium.

Chess

Can we apply the above result to chess? Not yet. Although there are only finitely many positions, it is an infinite game because positions can repeat.

How about making a new rule saying that repeating a position ends the game in a draw? I think it should work. If you can win with this new rule, then you have forced a win without repeating a position, which is a win without the new rule. If no one can force a win with this new rule, then without the new rule, a player will repeats a position (if not, somebody can force a win with the new rule). Afterward, someone will repeats a position again (if not, the first position that was repeated doesn’t actually need to be repeated for someone to force a win, i.e. someone can force a win with the new rule). So we see it has to go on forever, which is really a draw.