Further Results on Minimal Surfaces

Example 4.1
Example 4.2
Theorem 4.3
Definition 4.4
Theorem 4.5
Corollary 4.6
Example 4.7
Example 4.8
Exercise 4.1

The mean curvature condition $H=0$ in the definition of minimal surfaces has an easy geometric implication. Since $k_1k_2=K$ and $\frac{k_1+k_2}{2}=H$ , where $k_i$ are principal curvatures, the Gauss curvature of minimal surfaces must be nonpositive. Using the definition of Gauss curvature, one can easily see that a small neighbourhood of any point $p$ on a minimal surface cannot be a `bump', for otherwise the Gauss curvature at $p$ would be positive. This agrees with our intuition that a bump can be `flattened out' to further reduce the surface area. In fact, locally minimal surfaces look like a `saddle' as shown below.

A saddle

A bump

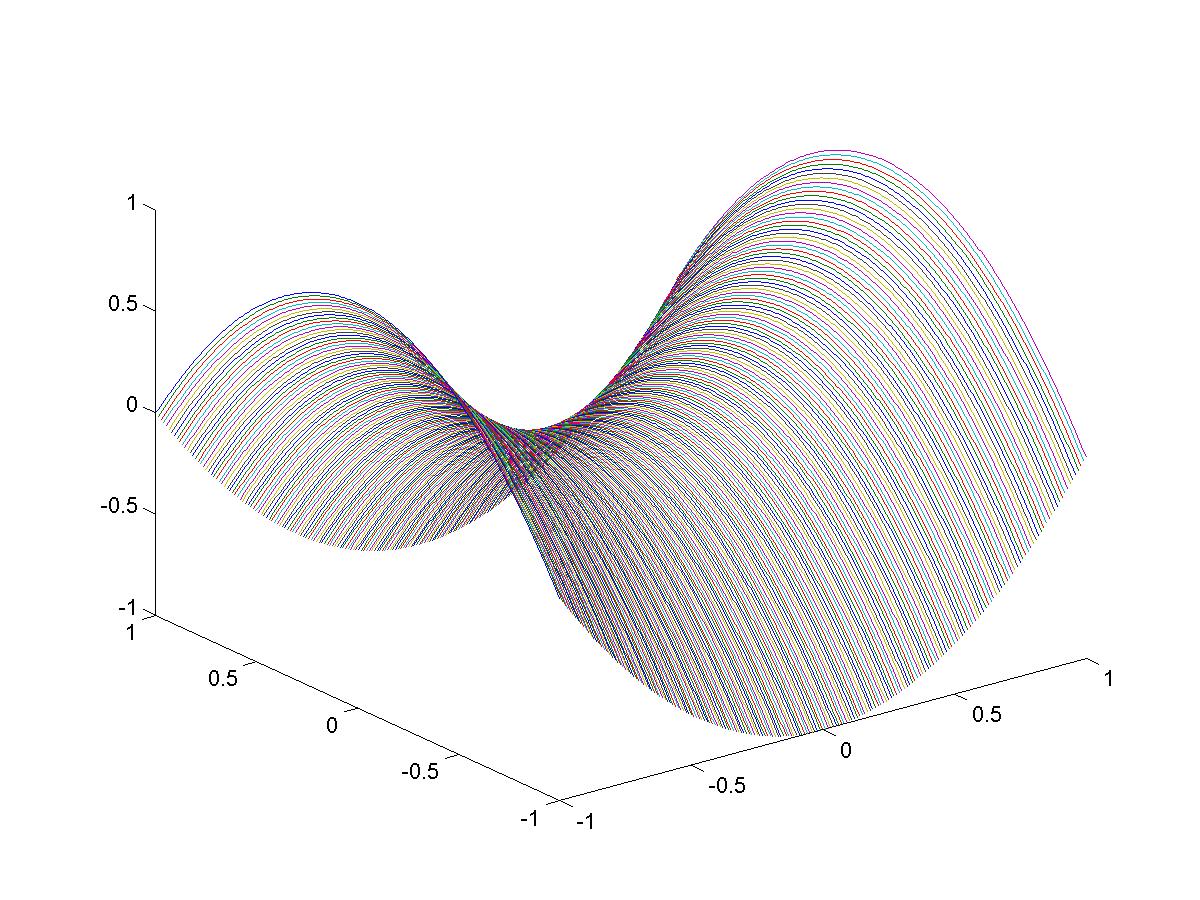
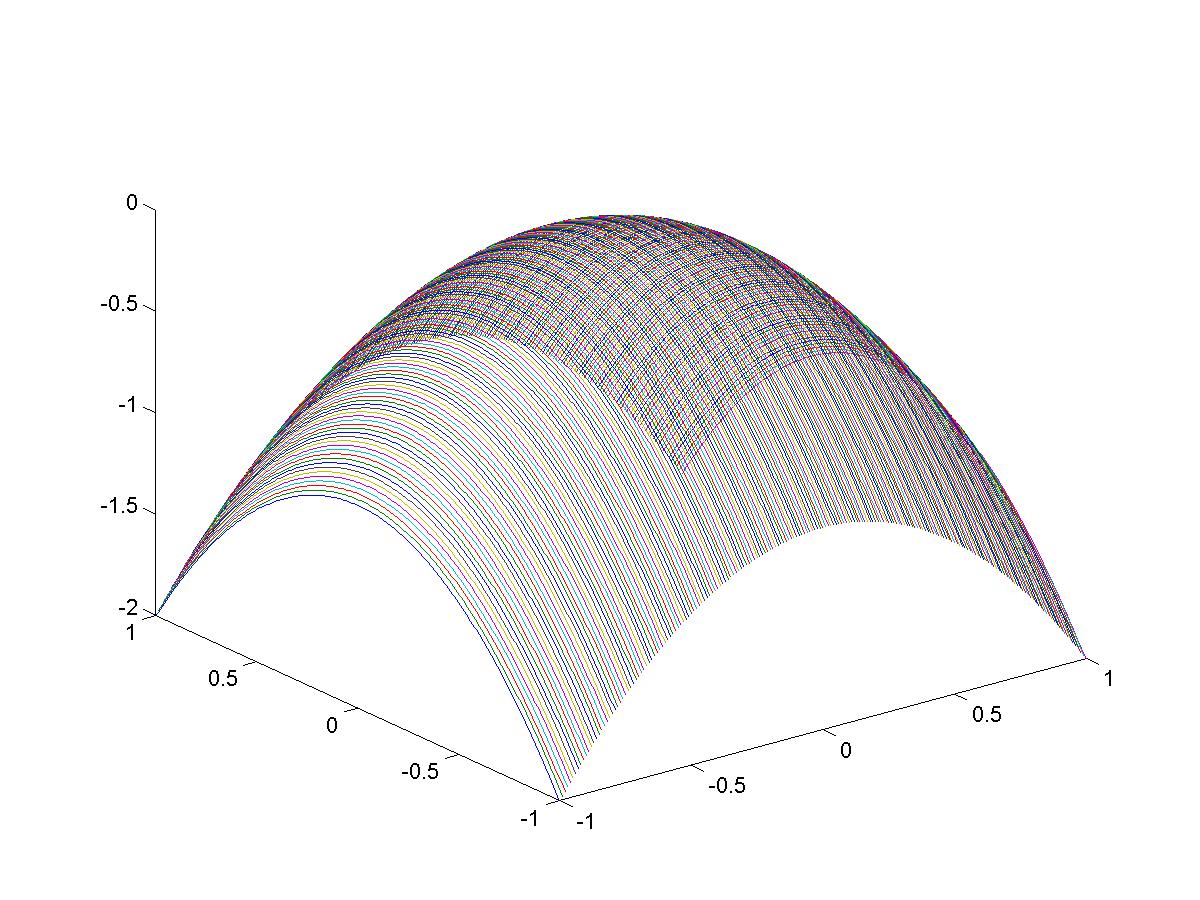
In the last section, we obtained the minimal surface equation, and remarked that it is in general hard to solve. But if we impose some additional conditions on the surface, the equation can be simplified such that it is solvable by elementary means.

Example 4.1 Scherk's surface. If we impose the condition that the smooth function $f(u, v)$ be separated, i.e. $f(u, v)=g(u)+h(v)$ , then the minimal surface equation becomes

$g''(u)(1+h'^2(v))+h''(v)(1+g'^2(u))=0$ $-\frac{1+g'^2(u)}{g''(u)}=\frac{1+h'^2(v)}{h''(v)}$ Since the LHS is a function of $u$ and the RHS a function of $v$ , both sides are actually constant. Let $-\frac{1+g'^2(x)}{g''(x)}=c\neq 0$ Putting $g'=p$ , $\begin{align*} -\frac{1+p^2}{p'}&=c\\ \frac{dp}{du}&=-\frac{1+p^2}{c}\\ -\frac{c}{1+p^2}dp&=du\\ \int-\frac{c}{1+p^2}dp&=\int du\\ -c\tan^{-1}p&=u\ \ \text{(let the constant of integration be 0)}\\ p&=-\tan\frac{u}{c} \end{align*}$ Integrating again, $g=\int pdx=c\log\cos\frac{u}{c}$ Similarly, $h=-c\log\cos\frac{v}{c}$ . So $f(u, v)=g(u)+h(v)=c\log\frac{\cos\frac{u}{c}}{\cos\frac{v}{c}}$ .

Scherk surface

Example 4.2 Assume that a minimal surface is a surface of revolution around the $z$ -axis. Its equation is given by

$\vec{x}(u, v)=(p(u)\cos v, p(u)\sin v, q(u))$ We may suppose further that the curve $(p(u), q(u))$ can be represented by $(f(u), u)$ for some smooth function $f$ . By Example 2.19, $f'^2+1=ff''$ The above equation appears to be difficult to solve, but we can use the following trick. Observe that $f''=\frac{df'}{du}=\frac{df}{du}\frac{df'}{df}=f'\frac{df'}{df}$ Now $\begin{align*} f'^2+1&=ff'\frac{df'}{df}\\ \frac{df}{f}&=\frac{f'df'}{f'^2+1}\\ \int\frac{df}{f}&=\int\frac{f'df'}{f'^2+1}\\ \log f&=\frac{1}{2}\log(f'^2+1)\ \ \text{(let the constant of integration be 0)}\\ f^2&=f'^2+1\\ \frac{df}{du}&=\sqrt{f^2-1}\\ \frac{df}{\sqrt{f^2-1}}&=du\\ \int\frac{df}{\sqrt{f^2-1}}&=\int du\\ \log(f+\sqrt{f^2-1})&=u\ \ \text{(again let the constant of integration be 0)}\\ f&=\frac{e^u+e^{-u}}{2}=\cosh u \end{align*}$ which represents the catenoid.

In fact, one can show that

Theorem 4.3 A surface of revolution which is also minimal is a part of either a plane or a catenoid.

Because of the mean curvature condition $H=0$ , there is a nice coordinate expression for minimal surfaces if conformal parametrization is used.

Definition 4.4 $\vec{x}$ is a conformal parametrization if $E=G$ , $F=0$ .

Theorem 4.5 Suppose $\vec{x}(u, v), (u, v)\in I_1\times I_2$ is a conformal parametrization with $E=G=\lambda$ . Then

$\vec{x}_{uu}+\vec{x}_{vv}=2H\lambda$

Proof By assumption,

$\langle\vec{x}_u, \vec{x}_u\rangle=\langle\vec{x}_v, \vec{x}_v\rangle=\lambda$ Differentiating with respect to $u$ , $\langle\vec{x}_{uu}, \vec{x}_u\rangle=\langle\vec{x}_{vu}, \vec{x}_v\rangle=\langle\vec{x}_{uv}, \vec{x}_v\rangle$ $\langle\vec{x}_u, \vec{x}_v\rangle=0$ implies that $\langle\vec{x}_{uv}, \vec{x}_v\rangle+\langle\vec{x}_u, \vec{x}_{vv}\rangle=0$ . So $\langle\vec{x}_u, \vec{x}_{vv}\rangle=-\langle \vec{x}_{uv}, \vec{x}_v\rangle$ Adding the two equations yields $\langle\vec{x}_{uu}+\vec{x}_{vv}, \vec{x}_u\rangle=0$ Similarly, $\langle\vec{x}_{uu}+\vec{x}_{vv}, \vec{x}_v\rangle=0$ . It follows that $\vec{x}_{uu}+\vec{x}_{vv}$ is perpendicular to the tangent plane, i.e. a scalar multiple of $N$ . Let $\vec{x}_{uu}+\vec{x}_{vv}=kN$ for some $k$ . Then $\begin{align*} k&=\langle kN, N\rangle\ \ (N\text{ is a unit vector})\\ &=\langle\vec{x}_{uu}+\vec{x}_{vv}, N\rangle\\ &=e+g \end{align*}$ On the other hand, $\begin{align*} 2H\lambda&=2\frac{Eg+Ge-2Ff}{2(EG-F^2)}\lambda\\ &=\frac{\lambda(e+g)}{\lambda^2}\lambda\\ &=e+g \end{align*}$ The result follows.

If a function $f$ satisfies $\frac{\partial^2 f}{\partial u^2}+\frac{\partial^2 f}{\partial v^2}=0$ , it is called a harmonic function.

Corollary 4.6 Let $\vec{x}$ be a conformal parametrization. $\vec{x}$ is minimal iff $\vec{x}_{uu}+\vec{x}_{vv}=0$ , i.e. the coordinate functions $x$ , $y$ and $z$ are harmonic.

Example 4.7 The parametrization of catenoid given in Example 2.9 is shown to be conformal in Example 3.4. Observe that

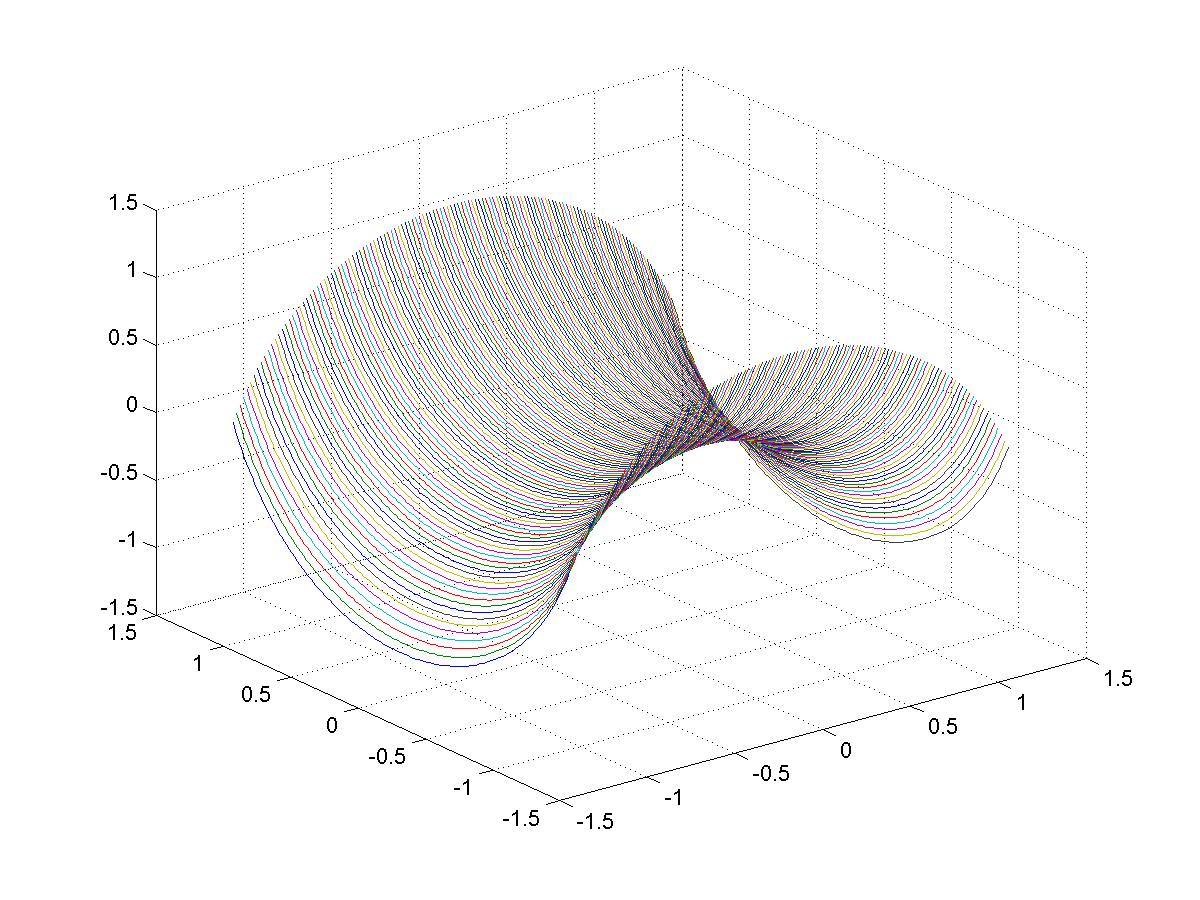
$\begin{align*} \left(\frac{\partial^2}{\partial u^2}+\frac{\partial^2}{\partial v^2}\right)(\cosh u\cos v)&=\cosh u\cos v-\cosh u\cos v\\ &=0\\ \left(\frac{\partial^2}{\partial u^2}+\frac{\partial^2}{\partial v^2}\right)(\cosh u\sin v)&=\cosh u\sin v-\cosh u\sin v\\ &=0\\ \left(\frac{\partial^2}{\partial u^2}+\frac{\partial^2}{\partial v^2}\right)u &=0 \end{align*}$ So by Corollary 4.6 the catenoid is a minimal surface.

Example 4.8 The parametrization of Enneper surface given in Example 3.5 is conformal. Observe that

$\begin{align*} \left(\frac{\partial^2}{\partial u^2}+\frac{\partial^2}{\partial v^2}\right)\left(u-\frac{1}{3}u^3+uv^2\right)&=\frac{\partial}{\partial u}(1-u^2+v^2)+\frac{\partial}{\partial v}(2uv)\\ &=-2u+2v\\ &=0\\ \left(\frac{\partial^2}{\partial u^2}+\frac{\partial^2}{\partial v^2}\right)\left(-v+\frac{1}{3}v^3-vu^2\right)&=\frac{\partial}{\partial u}(-2uv)+\frac{\partial}{\partial v}(-1+v^2-u^2)\\ &=-2v+2v\\ &=0\\ \left(\frac{\partial^2}{\partial u^2}+\frac{\partial^2}{\partial v^2}\right)(u^2-v^2)&=\frac{\partial}{\partial u}(2u)+\frac{\partial}{\partial v}(-2v)\\ &=2-2\\ &=0 \end{align*}$

Exercise 4.1 Show that $\vec{x}(u, v)=(-\sinh u\sin v, \sinh u\cos v, -v)$ is a minimal surface using Corollary 4.6. Note: This is another parametrization of helicoid.
Solution