Remember the example of a circuit board as a graph?  We noted that in circuit boards, none of the “edges” between the different parts of the circuit board could ever touch.  This is important to prevent charge running along one connection doesn’t just pass into another.  Not all graphs, however, can be arranged this way - namely, they can’t be made to lie flat with no edges crossing.

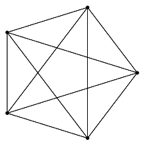
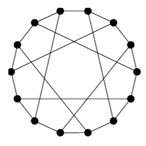
Looking at the graphs below, figure out which of the following can be made to lie flat in the plane.  (Graphs where we can do this are called “planar” graphs.)

Some of them were easy, others weren’t so easy.  Not many of these graphs were planar.  Did you notice anything odd about the last four graphs?

Exercise:  Given three houses (House A, B, and C) and three utilitites (Water, Electric, Gas,) can you connect all three of the houses to all three of the utilities without every crossing a pipeline?

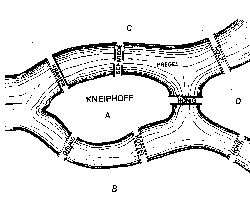
Exercise:  The “Bridges of Koenigsberg” Problem, as posed by Leonard Euler:

Given two islands in the middle of the river, connected to the mainland and each other by seven bridges as seen below, can someone go on a stroll so that they cross every bridge exactly once and end up back where they started?

Some classes of planar graphs are very easy to describe, and there are fun combinatorial ways of counting them.  One of the most famous is the following:

Given a n-sided polygon (a graph with n edges between n vertices making a single closed loop,) we can easily embed this as a planar graph.

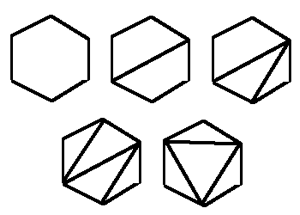
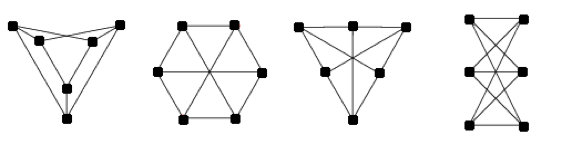
Any polygon can be broken up in to triangles by drawing edges between vertices at least two apart in the cycle, continuing in a way that never crosses previously drawn edges.  Eventually, the polygon graph will only contain triangles:

In this picture, the first four are iterations of a particular triangulation.  In the last one, it is just a different example of a triangulation.

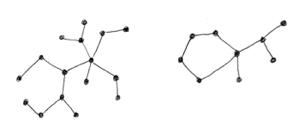
Examples:  Another class of graphs that we will regularly encounter fall into a group called “trees.”  A graph is a tree if it is connected (any two vertices in the graph can be connected by some “walk” along some number of edges,) and has no circuits (you cannot start at a vertex, “walk” away down an edge, and get back to that vertex without passing over the first edge.)

In the picture above, the first graph is a tree while the second graph is not (we can see a cycle of length five showing up there.)  These trees have some nice properties that make them easy to count - and as you can see from drawing a few examples, we can always represent a tree as  planar graph, so these are particularly nice.

Exercise:  Given a tree with q edges and p vertices, show that p=q+1.  [Hint:  What happens when you put down your first edge?  What about when you add another edge?  Remember that your tree must be connected.]

Determining whether a graph is planar or not isn’t trivial from its original representation.  While there are things we can see about a graph that would immediately tell us that it can’t be planar, there are a number of graphs that the proof of non-planarity is quite difficult.  We will return to this in a later lesson.