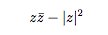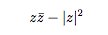(a+bi)*c=(a+bi)*(c+0i)=ac+bci

so geometrically, multiplication be a real number, c, changes its length but not its direction (i.e., its Arg).



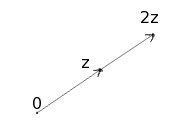
Since multiplication is determined by addition of angles and multiplication of lengths, it follows that there is only one complex number z for every pair of complex numbers w,u, neither of which are 0, so that

wz=u.

We should be able to define division then. First, we'll need a complex number q so that

qz=1.

What could this be?

Hint: compute