3. The approach to infinity

In 1959 Escher would write that: "as long as there have been men [...] upon this globe [...] we have held firmly to the notion of [...] all of which must continue to be everlasting in time and infinite in space". He was very interested in finding new ways of depicting the idea of infinite space, and the idea that he found and later developed is depicted in "Development II" (1939). Here "the figures used to construct this picture are subjected to a constant radial reduction in size, working from the edges toward the center, the point at which the limit is reached of the infinitely many and the infinitely small" (Escher)

Another example in the same direction is the wood engraving from 1956 "Smaller and smaller I". The figures no only get small in the center, but they are also metamorphosing, up to the point where they become unidentifiable.

His works in this direction can be grouped into three parts:

  • Square-Division Prints

    • They are the starting point and simple in construction. A few examples: "Smaller and Smaller I" (1956), " Plane Filling" (1957),"Square Limit" (1964)

  • Spiral Prints

    • The purpose of these is not so much to represent inifinty as to depict an expansion from infinitely small to infinitely large, and back to small again (birth, growth, decline in a cyclic way). Some examples: "Development II", "Path of Life I and II" (1958),"Path of Life III" (1966), "Butterflies"(1950), "Whirlpools"

  • The Coxeter Prints

    • After discovering a diagram in a book by the Canadian mathematician H.S.M. Coxeter, Escher built his famous "Circle Limit" series (I-IV) and "Snakes"(1969). These are the works that interests mathematician the most, because they are related to representing the hyperbolic plane using the Poincare model.


Geometry behind "Square Limit"

"Square Limit" is a woodcut from 1964.

Square Limit (woodcut - 1964)

It uses a very simple geometric procedure, that can be easily understood. Consider a right-angled triangle isosceles ABC. We build two more right-angled isosceles triangles, DBE and DCE, which are drawn on the side BC. The procedure is repeated and we get the triangles 3,4,5,6 and so on. See the figure:

Fig 1: The construction of triangles


The process can be continued infinitely, and we notice that if the initial square EFCD is one inch in side length, those immediately below have 1/2 inch, those below again 1/4 inch and so on. We also know that 1/2+1/4+1/8+1/16+...=1. Therefore CG=2 inch, and nevertheless we find an infinitely number of squares continually diminishing in size.
Escher didn't stop here, instead he filled each of the triangles with a lizard. In the figure you can see his steps: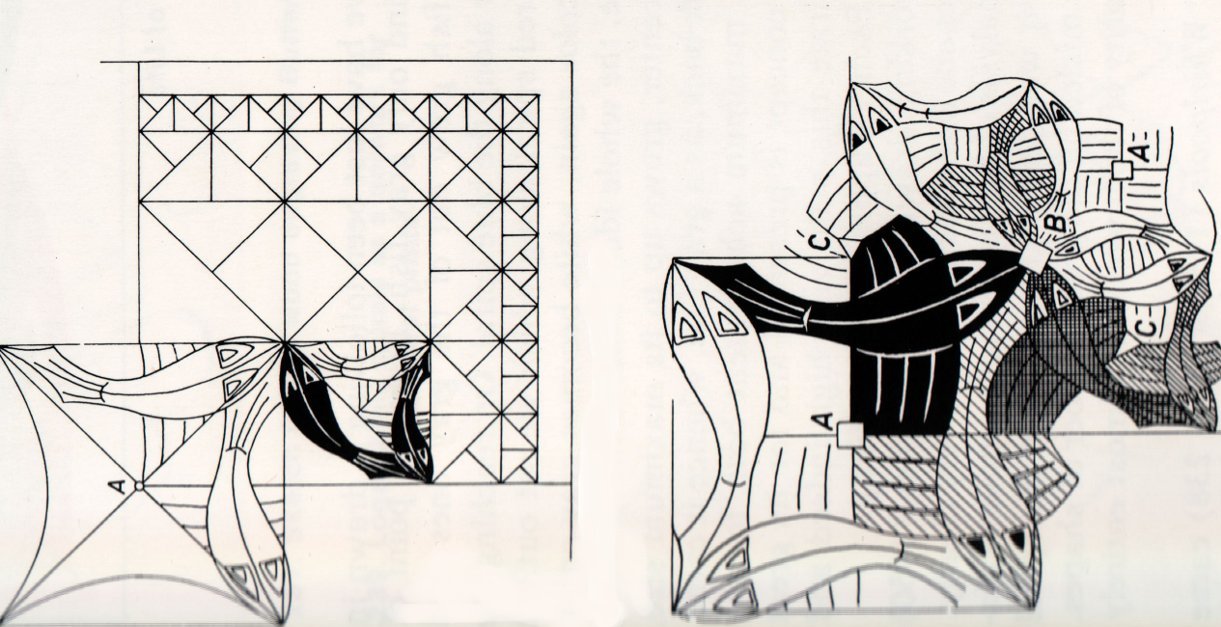


Fig 2: The building of "Square Limit"


The Coxeter Prints and Hyperbolic Geometry

The works from this category consist of the series of "Circle Limit":

  • "Circle Limit I"
  • "Circle Limit II"
  • "Circle Limit III"
  • "Circle Limit IV"
Escher discovered the following illustration in a math book by H.S.M. Coxeter:

Fig 3: The Coxeter illustration


He immediately recognized in it new ways to his approach to infinity. And this is his first "Circle Limit":


Fig 4: "Circle Limit I"


The purpose of the illustration in Coxeter's book was to explain the Poincaré model for the hyperbolic plane. But for this, we need first some background.


INDEX
NEXT