|
4. Euclidean and non-euclidean geometry
Until the 19th century Euclidean geometry was the only known system of geometry concerned with measurement and the concepts of congruence, parallelism and perpendicularity. Then, early in that century, a new system dealing with the same concepts was discovered. The new system, called non-Euclidean geometry, contained theorems that disagreed with the Euclidean theorems.
Review of Euclidean geometryEuclid stated ten assumptions (and many definitions) as his basis for proving all theorems (five postulates and five axioms), as follows: Euclid's Postulates
Euclid's Axioms (Common Notions)
Example
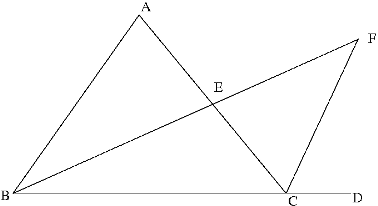
Let's prove proposition 16 from Euclid's "Elements": In any triangle, if one of the sides is extended, the exterior angle is greater than either of the opposite interior angles.
Let But, the whole being greater than any of its parts (axiom 5), we get that:
ExercisesUsing only the axioms above prove the following propositions from Euclid's "Elements":
The reader might wonder why he cannot recall Postulate 5 from previous studies. This is because in the present textbooks, an equivalent version is used: "through a point not on a given line there passes a unique parallel to the line". This is the "problem" postulate: there have been attempts to prove it using the previous postulates, as well as to disprove it. Arabs, Italians, Frenchman, Englishmen tried to prove it over the centuries, but no genuine solutions were obtained.
One of the first interesting works on this subject was the work of the logician and Jesuit priest Girolamo Saccheri (1667 - 1733). His idea was to take a quadrilateral ABCD, in which sides AD and BC are equal, and perpendicular to the base AB. He proved that the angles at C and D (called "summit angles") are equal. They are either right, obtuse or acute. 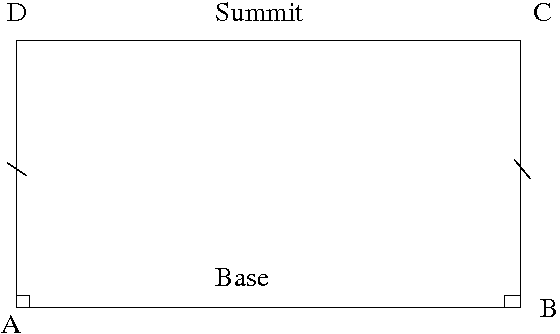
To assume that they are either obtuse or acute is to deny that Postulate 5 holds. So his plan was to assume, in turn, that they are either obtuse or acute, be led in each case to a contradiction, infer that they are therefore right angles, and go on to deduce Postulate 5 from this fact. He succeeded in showing that the obtuse case leads to a contradiction (if the summit angles were obtuse, the angle sum of the quadrilateral would be more than 360 degrees, which is a contradiction). However hard he tried, he could not get a contradiction for the other case. He deduced many strange results, but not a contradiction. Saccheri, in fact, discovered non-Euclidean geometry.
ExercisesConsider the Saccheri quadrilateral, and denote with F and G the midpoints of AB and CD. Using Euclid's postulates, prove the following:
Saccheri's work attracted considerable attention, and some mathematicians grasped the idea that the fifth postulate cannot be demonstrated (G. S. Klügel, J.H. Lambert). The last notable attempts to prove the postulate were those of A.M. Legendre (1752 - 1833), the famous French mathematician. He brought simplified and clearer proofs, without knowing Saccheri's work. His approach was to try to prove that the sum of the angles of a triangle is 180 degrees, and, in order to do that, he tried to get contradictions by assuming that the sum is larger or less than 180 degrees, but failed to get a clear contradiction. The birth of non-Euclidean geometryAfter understanding that the way to move further in geometry is not to try to prove the 5th postulate, but to negate it, mathematicians found a new type of geometry, called non-Euclidean geomtry. The first mathematicians that tried this approach were Janos Bolyai, Carl F. Gauss and Nikolai I. Lobachevsky. Nikolai I. Lobachevsky was the first to actually publish an account of non-Euclidean geometry in 1829. The work, being published in Russian, didn't find any responses in Europe, but Lobachevsky was persistent, and in 1840 he published a treatise in German, which he sent to Gauss. Gauss was very impressed with the work, and he recommended that the Russian mathematician be elected in the Göttingen Scientific Society. Janos Bolyai published his discoveries as an appendix to a book written by his father, Farkas. The latter sent a copy to his friend, C.F. Gauss, who was pleasantly surprised to see that someone else, besides him, thought about a new approach to geometry. He didn't want to publish it further or help Janos Bolyai to develop his ideas. Gauss anticipated some of Bolyai's discoveries, but he was afraid to make public his discoveries. Nevertheless he acknowledged the work of the two. Bolyai and Lobachevsky developed the subject much further than Gauss and their result were amazingly similar, although the methods were different. Both attacked plane geometry via the "horosphere" in three-space (the limit of an expanding sphere when its radius tends to infinity). They showed that geometry on a horosphere, where lines are "horocycles" (limits of circles on a sphere), is Euclidean. They both build a mapping from the sphere to the non-Euclidean plane to derive formulas for non-Euclidean trigonometry. After Gauss' death in 1855, when his correspondence was published, the mathematical world began to take non-Euclidean ideas seriously. Some of the best mathematicians of that time (Beltrami, Klein, Poincaré, Riemann). Bernhard Riemann, who was a student of Gauss, had the most profound insight into the geometry. He invented "elliptic geometry", which is different from the geometry of Bolyai and Lobachevsky, which is "hyperbolic". Since hyperbolic geometry is connected to Escher's work, this is the one that we will focus on. |