8. Escher's Tessellations of the plane

No other theme has been as popular in Escher's work as the periodic drawing division, which is related to the mathematical concept of tesselation of the plane. He himself was saying that: "it is the richest source of inspiration that I have ever tapped, and it has by no means dried up yet". Here is one of his first attempts:


Fig 1: First attempt at regular division of a plane, with imaginary animals (1926 or 1927)


He had a predisposition to the discovery and application of the priciples of tessellation, as it can be seen from early works (while he was studying under de Merquita in Haarlem). The idea of covering the entire surface with figures was not due to the influence of his mentor. The most detailed and fully developed production from this period is the woodcut "Eight Heads" (1922). Eight different heads are shown, four of them right way up, and four upside down. The heads have a theatrical air about them, false, unreal, "fin du siècle".

"Eight Heads" (woodcut, 1922)
The same print, turned 180 degrees

Fig 2: "Eight Heads" (up and down)


Then, in 1926, having some acquaintance with the Alhambra on the occasion of a brief visit, Escher was impressed by the Moorish frescos, although not all of them had figures that are true tessellations. He made his own sketches, as one can see in the next figure:


Fig 3: Sketches made in the Alhambra, pencil and coloured crayon (1936)


He wasn't satisfied by his results, so for 10 years he wasn't interested anymore in this topic. But in 1936, accompanied by his wife, he paid another visit to the Alhambra. For the second time he was impressed by the enormous possibilities lying in the division of a plane surface. He made copies, together with his wife, of the Moorish tessellations, and on his return home he studied them closely. He read books about ornamentation, and mathematical treatises he could not understand, although he liked and used the illustrations they had. He build his own system and wrote about it in 1941 and 1942.

Principles of Plane Tessellations

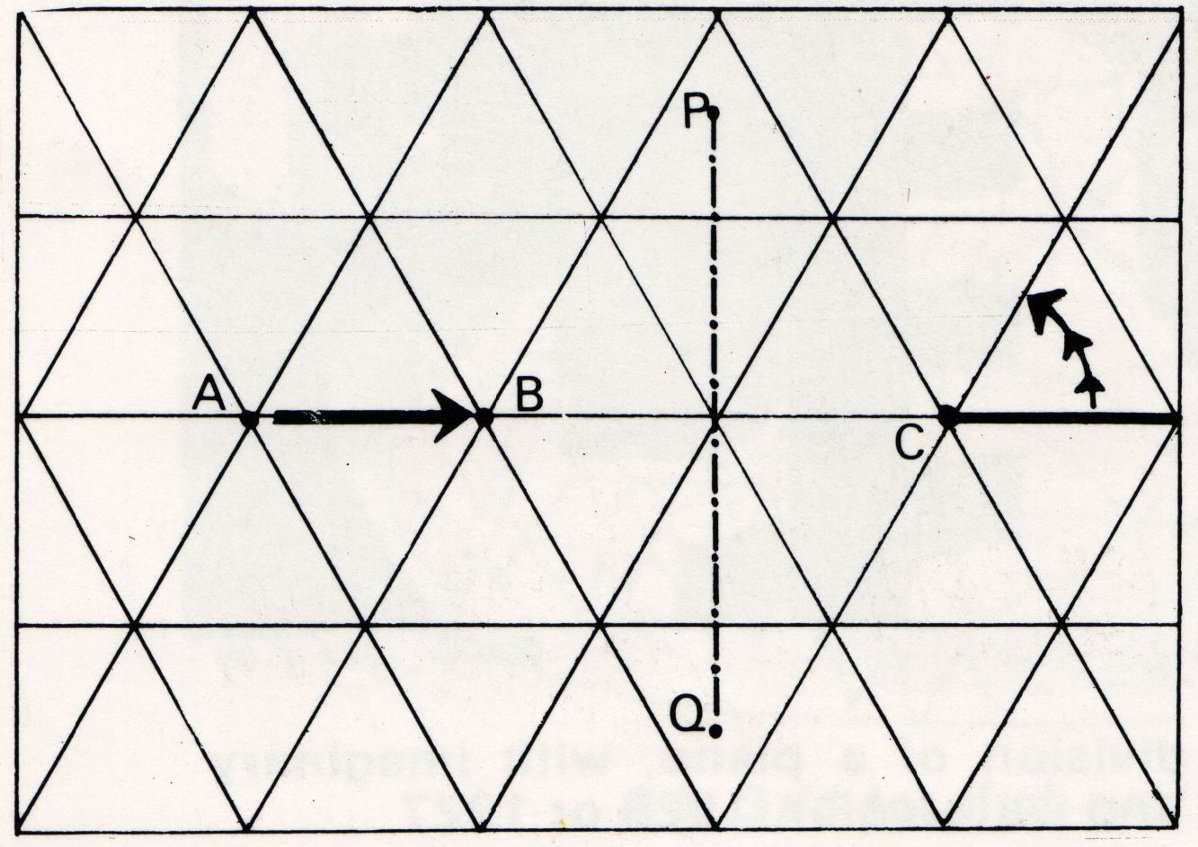
In the next figure, there is a simple design. The whole surface is covered with equilateral triangles. If we shift the whole plane over the distance AB, it will cover the underlying pattern once again. This is a translation of the plane. We can also turn the duplicate through 60 degrees about the point C, and we notice that again it covers the original pattern exactly. This is a rotation. Also if we do a reflection about the line PQ, the pattern remains the same.


Fig 4: Possible movements in a flat surface (translation, rotation, reflection)


A pattern can be made to map to itself by means of translation, rotation, reflection and glide reflection. There are 17 different groups of patters. Each groups admits only some kinds of shifts whereby they map onto themselves (some admit only translation, others translation and reflection etc.). Escher discovered all these possibilities without any previous mathematical knowledge. A particular characteristic of Escher's tessellation is that he chooses motifs that represent concrete objects or beings.

Making a Tessellation and a Metamorphosis

If you want to play and make your own tessellations, here is a great site: www.tessellations.org.

We will show you here the steps done by Escher to create one of his "Metamorphosis". First note that for Escher tessellations were just a means to an end, they were never produced as a main theme. They were included in different prints. The most use of periodic surface-division is found in two themes: metamorphosis and cycles. The metamorphoses consist of abstract shapes changing into sharply defined concrete forms, and then changing back again (a bird changing into a fish, a lizard into a honeycomb). Some examples are: "Metamorphosis I" (1937), "Day and Night" (1938), "Metamorphosis II" (1939). But most of the prints display not only metamorphoses, but also a cycle (like "Cycle" (1938)).

"Part I
Part II

Fig 5: "Metamorphosis II" (woodcut, 1939-1940) - split in two


Escher explains in his book "Plane Tessellations" (1958) the way how he brings a metamorphosis into being. We will use his "Regular division of the plane I" (1957) to explain all the steps.


Fig 6: A drawing showing the creation of a metamorphosis
  • Step 1-4: The surface is divided into (black and white) parallelograms.
  • Step 5: The boundaries of the parallelograms are changing, in such a way that an outward bulge on one side is balanced with an equal-sized inward bulge in the opposite side.
  • Step 6-7: There is a progressive alternation, not in the nature or position of the bulges, but in their size. The shape arrived at in step 7 is preserved until the end. Now the shape is filled with more and more details.
  • Step 8: Details are added to the black regions to signify birds.
  • Step 9-10: Details are added to the white regions also, to signify birds.
  • Step 11-12: More details are added (an eye and a beak are drawn into the tails), and each bird becomes a fish.


A similar, but more complex process, is found in "Metamorphosis II", which is the larges Escher print (20 cm high, and 4 meters long) - see above.

Other examples

Here is a tessellation, which was used in his most famous wood-cut, "Day and Night" (1938).

The periodic space filling that forms the basis for "Day and Night"
"Day and Night" (woodcut, 1938)

Fig 7: The tessellation and the final result for "Day and Night"


And another tessellation, which was used in "Cycle" (1938) - there is a metamorphosis from a human figure to geometric pattern, which changes to a diamond form, and then the diamonds go to make up a block that is used as building material and thereupon, within some secret chamber of the house, the lifeless shapes probably change into the cheerful young fellow:

The periodic space filling that forms the basis for "Cycle" (India ink, pencil, 1938)
"Cycle" (lithograph, 1938)

Fig 8: The tessellation and the final result for "Cycle"


Finally, his famous "Angels and Devils" (1941), which was also done in the Poincaré disk:

Periodic space filling for "Angles and Devils" (1941)
"Circle Limit IV" (woodcut, 1960)

Fig 8: The tessellation and the final result for the hyperbolic tiling for "Angels and Devils"


INDEX
NEXT