|
|
Conjugacy in a family of free-by-cyclic groups
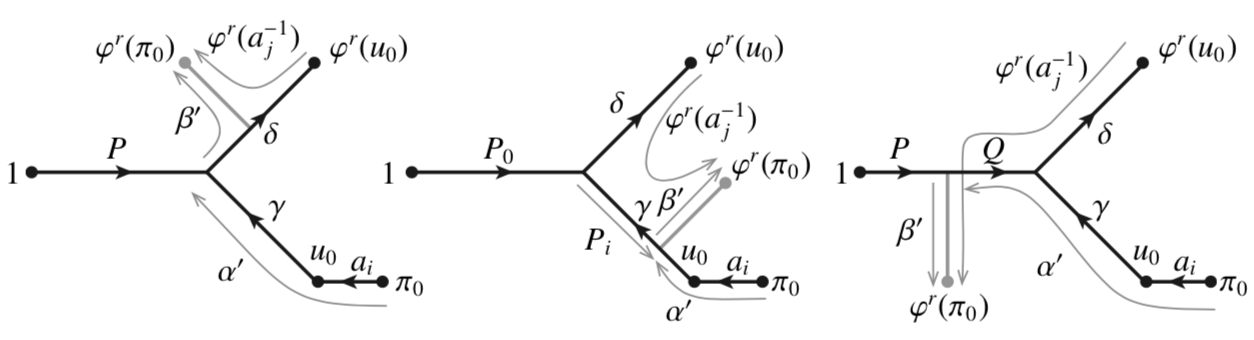
Martin Bridson, Timothy Riley, and Andrew Sale We analyse the geometry and complexity of the conjugacy problem in a family of free-by-cyclic groups $H_m=F_m \rtimes \mathbb{Z}$ where the defining free-group automorphism is positive and polynomially growing. We prove that the conjugator length function of $H_m$ is linear, and describe polynomial-time solutions to the conjugacy problem and conjugacy search problem in $H_m$.
|