Sampling Distributions
|
In day to day life we often think we know something about
a population when we've seen some of its members. In
statistics we examine information we get from a sample
more formally, and investigate its accuracy. Since every
sample is different ( we call this sampling variability
or sampling error ), a sample provides us with only a
hint about the true nature of the population.
In this lab, you will explore two situations, using
DataDesk to gain insight into how samples behave
and misbehave. In the first example, you will see how
percentages in samples may (or may not!) reveal the
percentage in the population - as with political polls.
In the second example, you will explore how the mean
of a sample reveals the mean of the population.
|
|
|
Case 1: Lyme Disease
Deer ticks live in forests and fields, attaching themselves to animals that pass by. Many of these ticks carry Lyme Disease, which is serious for humans, though it does not affect deer. In order to asses the danger to humans living or hiking in a region, it is important to know what percentage of the local deer ticks carry the disease. Since we could never collect them all, we must settle for examining a few ticks caught in insect traps. Could these few ticks give us reliable information about the overall risk level?
Open the datafile
Lyme. There you will find a variable named
Ticks. This variable models
10,000 ticks in a forest. Each tick is represented by
0 or
1, a
1 indicating that this tick carries Lyme disease and a
0 that it does not. Your task is to try to find out how widespread the disease is by selecting samples from this tick population.
- Here goes:
- Select the variable
Ticks. Under Manip, select Sample. We want to examine 20 ticks; that's 0.2% of the population. Draw 10 samples, but *do not* Create Sample Indices.
(Note: It is the sample size, here n = 20, that is important to us but DataDesk only allows you to specify the percentage to be sampled, .)
- Now select one of your sample icons, say
Ticks.1, and open it (double click). How many of your ticks carry the disease? What percentage of your sample is that?
- This number is called the sample proportion (notation
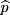 , read p-hat).
, read p-hat).
- Do you believe the population has exactly the same percentage as your sample?
- Under Calc, select Summaries - Reports. Notice that the mean adds up all the
1 's and 0 's and divides by the sample size. This is the sample proportion 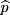 , the statistic you care about.
, the statistic you care about.
- Now let's examine the variability among your 10 samples. You can select all the sample icons at once by drawing a box around them with the mouse. Calc ulate Summaries As Variables. Select the icon for the Means. Open the variable. You are looking at the percentage of infected ticks found in each of your 10 samples. Note: they vary!
- Plot a Histogram of these sample proportions, and Modify the Scale (PlotScale) until it looks good. This is called the sampling distribution of the sample proportions.
- Describe what this indicates about the possible proportions of infected ticks which might show up in samples of size
20 drawn from this population. Discuss the shape, center and spread of this histogram.
- Reselect the population of
Ticks variable. Repeat the entire process, drawing 10 samples of n = 100 ticks each (1% of the population). Modify the Scale. Again describing the sampling distribution of sample proportions. (Beware: DataDesk may have changed the scale along the horizontal axis of the histogram; don't be misled.)
- Reselect the
Ticks population, and repeat again, drawing 10 samples of 1000 ticks this time.
- Compare these results. Carefully describe what happens to the shape, center and spread of the sampling distributions of sample proportions as the sample size increased. How accurately do you think you can now estimate the level of tick infestation in the entire population?
Case II: Health Costs
You work for an insurance company, where it is your job to set premiums for the health insurance plan. You need to know the typical (average) cost of treatment for heart attack patients. Since you cannot contact every hospital about every patient, you decide to pick a random sample, and use it to estimate the mean cost for the population.
- Open the datafile
HeartAttacks and select the variable Cost. These data are total hospital charges incurred by all heart attack patients in New York State a few years ago. Of course, that much information you would not really have available! But cheat a little... Take a look at a few of the numbers. Plot a Histogram. Describe what you see (shape, center and spread). Calc ulate the Summaries Report. How many patients were there? What was the true mean cost for their treatment?
- Now pretend you do not really know the true mean for that large set of data, and must discover it by taking a random sample of these patients. Generate
20 Samples, each 0.2% of the population. Select one of them, and Calc ulate the Summary Report. What's the sample size n? What is the mean of this sample? Check a few other samples. Are they equally accurate?
- Select all
20 samples at once (scroll to be sure you get them all), and Calc ulate Summaries as Variables. Make a histogram showing the sampling distribution of sample means. Modify the Scale, if necessary. Describe what you see (shape, center and spread).
- How might taking a larger sample help? Reselect the population
Cost, and choose 20 new samples of size n = 121 (1% of the population). How is this sampling distribution different? (Again, watch for rescaling of the x - axis.)
- Reselect the population again, and try an even bigger sample size - say
n = 607 (5% of the population). Describe the sampling distribution of sample means again.
- Summarize. How does the size of a sample impact the accuracy of the information the sample provides? What seems to happen to the shape, center and spread of the sampling distributions of sample means as sample size increases? You now have a glimpse of the most important result of all statistics: the Central Limit Theorem. You'll be studying that next week - and for the rest of the course!
To Turn in
- Answer the questions posed in the Exercises. Print out any graphs or summary tables you find helpful for your answers.
- Hand in your completed assignment when your lab TA asks for it near the start of lab next week.
- Remember to write down your section number and staple what you hand in.
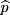 , read p-hat).
, read p-hat).
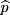 , the statistic you care about.
, the statistic you care about.

 Information
Information Staff
Staff Homework
Homework Lab Exercises
Lab Exercises Cool Tools
Cool Tools Fun Stuff
Fun Stuff